
| 人数 | 管理 | 技术开发 | 营销 | 生产 | 共计 |
| 老年 | 40 | 40 | 40 | 80 | 200 |
| 中年 | 80 | 120 | 160 | 240 | 600 |
| 青年 | 40 | 160 | 280 | 720 | 1 200 |
| 小计 | 160 | 320 | 480 | 1 040 | 2 000 |
分析 (1)用分层抽样方法从老年人、中年人和青年人中抽取对应的人数即可;
(2)用分层抽样法从管理层、技术开发部、营销部以及生产部抽取对应的人数即可;
(3)用分层抽样方法从老年人、中年人和青年人中抽取对应的人数即可.
解答 解:(1)因为总体是由差异比较明显的几部分组成,
所以要抽取40人调查身体状况,应用分层抽样方法,
从老年人中抽取40×$\frac{200}{2000}$=4人,
从中年人中抽取40×$\frac{600}{2000}$=12人,
从青年人中抽取40×$\frac{1200}{2000}$=24人;
(2)要开一个25人的讨论单位发展与薪金调整方面的座谈会,应用分层抽样法,
从管理层抽取25×$\frac{160}{2000}$=2人,
从技术开发部抽取25×$\frac{320}{2000}$=4人,
从营销部抽取25×$\frac{480}{2000}$=6人,
从生产部抽取25×$\frac{1040}{2000}$=13人;
(3)要抽取20人调查对广州亚运会举办情况的了解,应用分层抽样方法,
从老年人中抽取20×$\frac{200}{2000}$=2人,
从中年人中抽取20×$\frac{600}{2000}$=6人,
从青年人中抽取20×$\frac{1200}{2000}$=12人.
点评 本题考查了分层抽样方法的灵活应用问题,是基础题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2ln3) | B. | (ln2,2ln3) | C. | (ln2,+∞) | D. | (-∞,2ln3)∪(ln2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
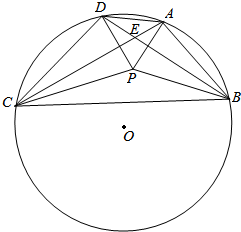 凸四边形ABCD的外接圆的圆心O,已知AC≠BD,AC与BD交于点E,若P为四边形ABCD内部一点,使得∠PAB+∠PCB=∠PBC+∠PDC=90°,求证:O,P,E三点共线.
凸四边形ABCD的外接圆的圆心O,已知AC≠BD,AC与BD交于点E,若P为四边形ABCD内部一点,使得∠PAB+∠PCB=∠PBC+∠PDC=90°,求证:O,P,E三点共线.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com