
���� ��1���������֪����2=4��cos�ȣ�����2=x2+y2��x=��cos�ȣ����뼴���������C1��ֱ�����귽�̣���ȥ����t���������ֱ��l����ͨ���̣�
��2�����PQ�е�M�����꣬���õ㵽ֱ�ߵľ��빫ʽ�������ǹ�ʽ���������Һ��������ʣ��������PQ���е�M��ֱ��l��������ֵ��
��� �⣺��1��������C1�ļ����귽��Ϊ��=4cos�ȣ����2=4��cos�ȣ�
�ɦ�2=x2+y2��x=��cos�ȣ�����������x2+y2-4x=0
����${C_1}��{x^2}+{y^2}-4x=0$��
��ֱ��l����t��ȥ���������ֱ��l��x+2y-3=0������5�֣�
��2����$P��2\sqrt{2}��\frac{��}{4}��$��ֱ������Ϊ��2��2����$Q��2cos����sin������M��1+cos����1+\frac{1}{2}sin����$��
��M��ֱ��l�ľ���d=$\frac{ح1+cos��+2��1+\frac{1}{2}sin����-3ح}{\sqrt{{1}^{2}+{2}^{2}}}$=$\frac{\sqrt{10}}{5}$حsin����+$\frac{��}{4}$��ح��
�����Һ��������ʿ�֪��0��حsin����+$\frac{��}{4}$��ح��1��
��PQ���е�M��ֱ��l�����ֵΪ$\frac{{\sqrt{10}}}{5}$������10�֣�
���� ���⿼��Բ�ļ����ֱ꣬�ߵIJ������̣�����㵽ֱ�ߵľ��빫ʽ��������������������е��⣮


 ѧҵ����һ��һ��ϵ�д�
ѧҵ����һ��һ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{8}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{3}{8}$ | D�� | $\frac{3}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | $\sqrt{4+\frac{��^2}{9}}$ | C�� | $\sqrt{1+\frac{��^2}{9}}$ | D�� | $\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-3$\sqrt{3}$��-3�� | B�� | ��3$\sqrt{3}$��-3�� | C�� | ��-3$\sqrt{3}$��3�� | D�� | ��3$\sqrt{3}$��3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| x | 2 | 3 | 4 | 5 | 6 | 7 |
| y | 4.1 | 2.5 | -0.5 | 0.5 | -2.0 | -3.0 |
| A�� | $\hat a��0��\hat b��0$ | B�� | $\hat a��0��\hat b��0$ | C�� | $\hat a��0��\hat b��0$ | D�� | $\hat a��0��\hat b��0$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
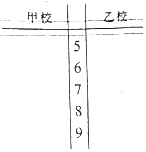 ij�жԴ����м�ʾ����ѧУ���ļס�������ѧУ���и������գ���ѧ����������һ���������������20λ������20λ�����������ѧУ�����֣�����Խ�߱������������Խ�ã����������£�
ij�жԴ����м�ʾ����ѧУ���ļס�������ѧУ���и������գ���ѧ����������һ���������������20λ������20λ�����������ѧУ�����֣�����Խ�߱������������Խ�ã����������£��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com