
分析 (1)利用递推关系、等比数列的性质即可得出p.
(2)①利用递推关系、等差数列的性质即可得出an.
②an=n,在n与n+1间插入n个正数,组成公比为qn的等比数列,故有$n+1=nq_n^{n+1}$,即${q_n}={(\frac{n+1}{n})^{\frac{1}{n+1}}}$,即${(\frac{n+1}{n})^{n+a}}≤e$,两边取对数得$(n+a)ln(\frac{n+1}{n})≤1$,分离参数得$a≤\frac{1}{{ln(\frac{n+1}{n})}}-n$恒成立.令$\frac{n+1}{n}=x$,x∈(1,2],则$a≤\frac{1}{lnx}-\frac{1}{x-1}$,x∈(1,2],令$f(x)=\frac{1}{lnx}-\frac{1}{x-1}$,x∈(1,2],利用导数研究其单调性极值与最值即可得出.
解答 解:(1)当n=1时,a1=pa1a2,${a_2}=\frac{1}{p}$,当n=2时,a1+a2=pa2a3,${a_3}=\frac{{{a_1}+{a_2}}}{{p{a_2}}}=1+\frac{1}{p}$,
由$a_2^2={a_1}{a_3}$得$\frac{1}{p^2}=1+\frac{1}{p}$,即p2+p-1=0,解得:$p=\frac{{-1±\sqrt{5}}}{2}$. …(3分)
(2)①由2a2=a1+a3得$p=\frac{1}{2}$,故a2=2,a3=3,所以${S_n}=\frac{1}{2}{a_n}{a_{n+1}}$,
当n≥2时,${a_n}={S_n}-{S_{n-1}}=\frac{1}{2}{a_n}{a_{n+1}}-\frac{1}{2}{a_{n-1}}{a_n}$,
因为an≠0,所以an+1-an-1=2…(6分)
故数列{an}的所有奇数项组成以1为首项2为公差的等差数列,
其通项公式${a_n}=1+(\frac{n+1}{2}-1)×2=n$,…(7分)
同理,数列{an}的所有偶数项组成以2为首项2为公差的等差数列,
其通项公式是${a_n}=2+(\frac{n}{2}-1)×2=n$…(8分)
所以数列{an}的通项公式是an=n…(9分)
②an=n,在n与n+1间插入n个正数,组成公比为qn的等比数列,故有$n+1=nq_n^{n+1}$,
即${q_n}={(\frac{n+1}{n})^{\frac{1}{n+1}}}$,…(10分)
所以${({q_n})^{(n+1)(n+a)}}≤e$,即${(\frac{n+1}{n})^{n+a}}≤e$,两边取对数得$(n+a)ln(\frac{n+1}{n})≤1$,
分离参数得$a≤\frac{1}{{ln(\frac{n+1}{n})}}-n$恒成立 …(11分)
令$\frac{n+1}{n}=x$,x∈(1,2],则$a≤\frac{1}{lnx}-\frac{1}{x-1}$,x∈(1,2],…(12分)
令$f(x)=\frac{1}{lnx}-\frac{1}{x-1}$,x∈(1,2],则$f'(x)=\frac{{{{(lnx)}^2}-\frac{{{{(x-1)}^2}}}{x}}}{{{{(lnx)}^2}{{(x-1)}^2}}}$,
下证$lnx≤\frac{x-1}{{\sqrt{x}}}$,x∈(1,2],
令$g(x)=x-\frac{1}{x}-2lnx,x∈(1,+∞)$,则$g'(x)=\frac{{{{(x-1)}^2}}}{x^2}>0$,所以g(x)>0,
即$2lnx<x-\frac{1}{x}$,用$\sqrt{x}$替代x可得$lnx<\frac{x-1}{{\sqrt{x}}}$,x∈(1,2],…(14分)
所以$f'(x)=\frac{{{{(lnx)}^2}-\frac{{{{(x-1)}^2}}}{x}}}{{{{(lnx)}^2}{{(x-1)}^2}}}<0$,所以f(x)在(1,2]上递减,
所以$a≤f(2)=\frac{1}{ln2}-1$…(16分)
点评 本题考查了等比数列的定义及其通项公式、递推式的应用、利用导数研究函数的单调性极值与最值,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
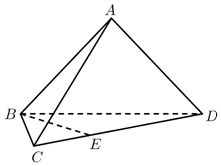 如图,在三棱锥A-BCD中,平面ABD⊥平面BCD,AB=AD,∠CBD=60°,BD=2BC=4,点E在CD上,DE=2EC.
如图,在三棱锥A-BCD中,平面ABD⊥平面BCD,AB=AD,∠CBD=60°,BD=2BC=4,点E在CD上,DE=2EC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
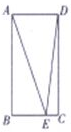 在如图所示的矩形ABCD中,AB=4,AD=2,E为线段BC上的点,则$\overrightarrow{AE}•\overrightarrow{DE}$的最小值为( )
在如图所示的矩形ABCD中,AB=4,AD=2,E为线段BC上的点,则$\overrightarrow{AE}•\overrightarrow{DE}$的最小值为( )| A. | 12 | B. | 15 | C. | 17 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 在△ABC中,D、E分别是AB、AC的中点,M是直线DE上的动点.若△ABC的面积为2,则$\overrightarrow{MB}$•$\overrightarrow{MC}$+$\overrightarrow{BC}$2的最小值为2$\sqrt{3}$.
在△ABC中,D、E分别是AB、AC的中点,M是直线DE上的动点.若△ABC的面积为2,则$\overrightarrow{MB}$•$\overrightarrow{MC}$+$\overrightarrow{BC}$2的最小值为2$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2π}{3}$ | B. | $\frac{4π}{3}$ | C. | 2π | D. | $\frac{8π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com