练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】将函数在区间内的全部极值点按从小到大的顺序排成数列．

    （1）求数列的通项公式；

    （2）设，数列的前n项和，求证：数列为等比数列，并求．

    【答案】（1）；（2）证明见解析，.

    【解析】

    （1）先利用三角函数的诱导公式及二倍角公式化简函数，令得极值点，判断出全部极值点按从小到大排列构成以为首项，为公差的等差数列，用等差数列的通项公式求出通项．
    （2）利用，求出,作商，利用等比数列的定义判断出是以为首项，为公比的等比数列，利用等比数列的通项公式求出通项，一步求出数列前项的和．

    (1)

    令，即

    所以函数的极值点为.

    从而函数在区间内的全部极值点按从小到大排列构成以以为首项，为公差的等差数列.

    所以数列

    （2）由可知对任意的正整数，都不是的整数倍.

    所以

    所以数列为等比数列.

    所以

    .

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】依据某地某条河流8月份的水文观测点的历史统计数据所绘制的频率分布直方图如图（甲）所示；依据当地的地质构造，得到水位与灾害等级的频率分布条形图如图（乙）所示.

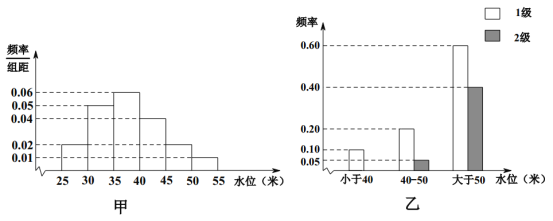
    （1）试估计该河流在8月份水位的众数；

    （2）我们知道若该河流8月份的水位小于40米的频率为f，该河流8月份的水位小于40米的情况下发生1级灾害的频率为g，则该河流8月份的水位小于40且发生1级灾害的频率为，其他情况类似.据此，试分别估计该河流在8月份发生12级灾害及不发生灾害的频率，，；

    （3）该河流域某企业，在8月份，若没受12级灾害影响，利润为500万元；若受1级灾害影响，则亏损100万元；若受2级灾害影响则亏损1000万元.现此企业有如下三种应对方案:

    方案

    防控等级

    费用（单位:万元）

    方案一

    无措施

    0

    方案二

    防控1级灾害

    40

    方案三

    防控2级灾害

    100

    试问，如仅从利润考虑，该企业应选择这三种方案中的哪种方案?说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设，且.

    (1)求a的值及f(x)的定义域；

    (2)求f(x)在区间上的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】经市场调查：生产某产品需投入年固定成本为万元，每生产万件，需另投入流动成本为万元，在年产量不足万件时，（万元），在年产量不小于万件时，（万元）.通过市场分析，每件产品售价为元时，生产的商品能当年全部售完.

    （1）写出年利润（万元）关于年产量（万件）的函数解析式；

    （2）当产量为多少时利润最大？并求出最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数,,是实数.

    （Ⅰ）若在处取得极值,求的值;

    （Ⅱ）若在区间为增函数,求的取值范围;

    （Ⅲ）在(Ⅱ)的条件下,函数有三个零点,求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，直线的参数方程为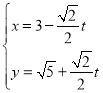(为参数)。在极坐标系(与直角坐标系取相同的长度单位，且以原点为极点，以轴正半轴为极轴)中，圆的极坐标方程为。

    （1）求直线的普通方程和圆的直角坐标方程；

    （2）设圆与直线交于，两点，若点的坐标为，求。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知△ABC的两个顶点A,B的坐标分别为(,0),(,0),圆E是△ABC的内切圆,在边AC,BC,AB上的切点分别为P,Q,R,|CP|=2,动点C的轨迹为曲线G.

    （1）求曲线G的方程;

    （2）设直线l与曲线G交于M,N两点,点D在曲线G上,是坐标原点,判断四边形OMDN的面积是否为定值?若为定值,求出该定值;如果不是,请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，直线的参数方程为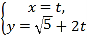（为参数），以原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为.

    （Ⅰ）写出直线的普通方程和曲线的直角坐标方程；

    （Ⅱ）已知点，直线与曲线相交于点，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】[选修4-4：极坐标与参数方程]

    在直角坐标系中，曲线的参数方程为（是参数），以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为.

    （1）求曲线的极坐标方程和曲线的直角坐标方程；

    （2）若射线 与曲线交于，两点，与曲线交于，两点，求取最大值时的值

    查看答案和解析>>

    同步练习册答案