
| A. | $\frac{\sqrt{2}}{6}$ | B. | -$\frac{\sqrt{2}}{5}$ | C. | -$\frac{\sqrt{2}}{10}$ | D. | $\frac{\sqrt{2}}{12}$ |
分析 根据题意表示出$\overrightarrow{O{P}_{1}}$•$\overrightarrow{O{P}_{2}}$,根据向量数量积的运算求得x1x2+y1y2=cosθ,进而根据sin(θ+$\frac{π}{4}$)的值,求得cosθ的值.
解答 解:由题意可得$\frac{π}{2}$<θ<π,sin($θ+\frac{π}{4}$)=$\frac{3}{5}$>0,
∴$θ+\frac{π}{4}$是钝角,∴cos($θ+\frac{π}{4}$)=-$\frac{4}{5}$,
依题意知$\overrightarrow{O{P}_{1}}$=(x1,y1)
$\overrightarrow{O{P}_{2}}$=(x2,y2),
则$\overrightarrow{O{P}_{1}}$•$\overrightarrow{O{P}_{2}}$=x1x2+y1y2,
另外P1(x1,y1),P2(x2,y2)在单位圆上,|$\overrightarrow{O{P}_{1}}$|=|$\overrightarrow{O{P}_{2}}$|=1
$\overrightarrow{O{P}_{1}}$•$\overrightarrow{O{P}_{2}}$=|$\overrightarrow{O{P}_{1}}$|•|$\overrightarrow{O{P}_{2}}$|cosθ=1•1•cosθ=cosθ,
∴x1x2+y1y2=cosθ,
∵cosθ=cos(θ+$\frac{π}{4}$-$\frac{π}{4}$)=cos(θ+$\frac{π}{4}$)cos$\frac{π}{4}$+sin(θ+$\frac{π}{4}$)sin$\frac{π}{4}$=$\frac{3}{5}$×$\frac{\sqrt{2}}{2}$-$\frac{4}{5}$×$\frac{\sqrt{2}}{2}$=-$\frac{\sqrt{2}}{10}$.
故选:C
点评 本题主要考查了是平面向量的运算,平面向量数量积的应用根据条件转化为向量数量积,以及利用两角和差的余弦公式是解决本题的关键,注重了对学生基础知识的考查.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
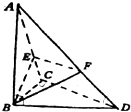 如图,在三棱锥A-BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是AC,AD上的动点.且$\frac{AE}{AC}$=$\frac{AF}{AD}$=λ(0<λ<1).
如图,在三棱锥A-BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是AC,AD上的动点.且$\frac{AE}{AC}$=$\frac{AF}{AD}$=λ(0<λ<1).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 19 | B. | 20 | C. | 21 | D. | 22 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若x,y∈R,且$\left\{\begin{array}{l}{x+y>4}\\{xy>4}\end{array}\right.$,则$\left\{\begin{array}{l}{x>2}\\{y>2}\end{array}\right.$ | |
| B. | △ABC中,A>B是sinA>sinB的充分必要条件 | |
| C. | 命题“若a=-1,则f(x)=ax2+2x-1只有一个零点”的逆命题为真 | |
| D. | 设命题p:?x>0,x2>2x,则¬p:?x0≤0,x02≤2x0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com