
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 根据题意,良马走的路程可以看成一个首项a1=193,公差d1=13的等差数列,记其前n项和为Sn,驽马走的路程可以看成一个首项b1=97,公差为d2=-0.5的等差数列,记其前n项和为Tn,由等差数列的通项公式以及其前n项和公式分析三个说法的正误,即可得答案.
解答 解:根据题意,良马走的路程可以看成一个首项a1=193,公差d1=13的等差数列,记其前n项和为Sn,
驽马走的路程可以看成一个首项b1=97,公差为d2=-0.5的等差数列,记其前n项和为Tn,
依次分析3个说法:
对于①、b9=b1+(9-1)×d2=93,故①正确;
对于②、S5=5a1+$\frac{5×4}{2}$×d1=5×193+10×13=1095;故②正确;
对于③、设第n天两马相遇,则有Sn+Tn≥6000,
即na1+$\frac{n(n-1)}{2}$d1+nb1+$\frac{n(n-1)}{2}$d2≥6000,变形可得5n2+227n-4800≥0,
分析可得n的最小值为16,
故两马相遇时,良马走了16日,故③错误;
3个说法中只有1个错误;
故选:B.
点评 本题考查等差数列的通项公式与求和公式,关键要熟悉等差数列的通项公式和前n项和公式.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{7}{6}$,+∞) | B. | (-∞,$\frac{7}{6}$) | C. | (-∞,$\frac{1}{3}$) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
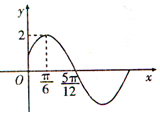
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12,-15 | B. | 5,-15 | C. | 12,-5 | D. | 5,-16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,e+$\frac{1}{e}$] | B. | [1,e-$\frac{1}{e}$] | C. | [e-$\frac{1}{e}$,e+$\frac{1}{e}$] | D. | [e-$\frac{1}{e}$,e] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
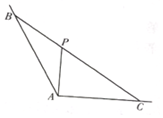 如图,∠BAC=$\frac{2π}{3}$,P为∠BAC内部一点,过点P的直线与∠BAC的两边交于点B,C,且PA⊥AC,AP=$\sqrt{3}$.
如图,∠BAC=$\frac{2π}{3}$,P为∠BAC内部一点,过点P的直线与∠BAC的两边交于点B,C,且PA⊥AC,AP=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({0,\frac{1}{4}}]$ | B. | $({\frac{1}{4},\frac{1}{2}}]$ | C. | $[{\frac{1}{4},\frac{1}{2}})$ | D. | $({0,\frac{1}{2}})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com