
分析 根据题意,分析可得A的元素为圆x2+y2=9的上半部分上的点,B的元素为直线y=x+b上的点,进而分析有若A与B的交集中有且只有一个元素,即x2+y2=9的上半部分圆与直线y=x+b只有一个交点,由直线与圆的位置关系分析可得答案.
解答 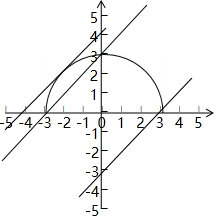 解:根据题意,$A=\left\{{({x,y})\left|{y=\sqrt{9-{x^2}}}\right.}\right\}$,其元素为圆x2+y2=9的上半部分上的点,
解:根据题意,$A=\left\{{({x,y})\left|{y=\sqrt{9-{x^2}}}\right.}\right\}$,其元素为圆x2+y2=9的上半部分上的点,
B={(x,y)|y=x+b},其元素为直线y=x+b上的点,
若A与B的交集中有且只有一个元素,即x2+y2=9的上半部分圆与直线y=x+b只有一个交点,
作图分析可得:b的取值范围为{b|-3≤b≤3或b=4};
故答案为:{b|-3≤b≤3或b=4}.
点评 本题考查直线与圆的位置关系,涉及集合的表示法以及交集的计算,关键是分析集合A、B的几何意义.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:高中数学 来源: 题型:解答题
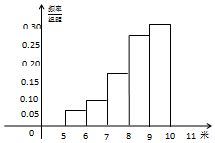 某市为了解今年高中毕业生的身体素质状况,从本市某校高中毕业班中抽取一个班进行实心球测试,成绩在8米及以上的为合格.把所得数据整理后,分成六组得到频率分布直方图的一部分(如图).已知前五个小组的频率分别为0.06.0.10,0.14,0.28,0.30.第六小组的频数是6.
某市为了解今年高中毕业生的身体素质状况,从本市某校高中毕业班中抽取一个班进行实心球测试,成绩在8米及以上的为合格.把所得数据整理后,分成六组得到频率分布直方图的一部分(如图).已知前五个小组的频率分别为0.06.0.10,0.14,0.28,0.30.第六小组的频数是6.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{6}}{4}$ | B. | $\frac{{\sqrt{10}}}{4}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{17}{18}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2<b2 | B. | a2b<ab2 | C. | D.$\frac{1}{a}$>$\frac{1}{b}$ | D. | 2a-2b<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
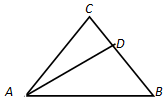
| A. | $\frac{2}{3}\overrightarrow a+\frac{1}{3}\overrightarrow b$ | B. | $\frac{2}{3}\overrightarrow a-\frac{1}{3}\overrightarrow b$ | C. | $\frac{1}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$ | D. | $\frac{2}{3}\overrightarrow a-\frac{2}{3}\overrightarrow b$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{4\sqrt{3}}}{3}$ | B. | $\frac{{8\sqrt{3}}}{3}$ | C. | 4 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com