
分析 利用数学归纳法及其组合数的运算性质、二项式定理即可证明.
解答 证明:利用数学归纳法证明:
①当n=1时,左边=a+b,右边=$C_1^0a{b^0}+C_1^1{a^0}b=a+b$,所以结论成立;
②假设当n=k(k≥1,k∈N*)时,结论成立,
则当n=k+1时,(a+b)k+1=(a+b)k(a+b)
=$({C_k^0{a^k}+C_k^1{a^{k-1}}b+C_k^2{a^{k-2}}{b^2}+…+C_k^r{a^{k-r}}{b^r}+…+C_k^k{b^k}})(a+b)$
=$({C_k^0{a^k}+C_k^1{a^{k-1}}b+C_k^2{a^{k-2}}{b^2}+…+C_k^r{a^{k-r}}{b^r}+…+C_k^k{b^k}})(a+b)$
=$({C_k^0{a^{k+1}}+C_k^1{a^k}b+C_k^2{a^{k-1}}{b^2}+…+C_k^r{a^{k+1-r}}{b^r}+…+C_k^ka{b^k}})$$+({C_k^0{a^k}b+C_k^1{a^{k-1}}{b^2}+C_k^2{a^{k-2}}{b^3}+…+C_k^r{a^{k-r}}{b^{r+1}}+…+C_k^k{b^{k+1}}})$
=$C_k^0{a^{k+1}}+(C_k^0+C_k^1){a^k}b+(C_k^1+C_k^2){a^{k-1}}{b^2}+…+(C_k^{r-1}+C_k^r){a^{k+1-r}}{b^r}$$+…+(C_k^{k-1}+C_k^k)a{b^k}+C_k^k{b^{k+1}}$(7分)
=$C_{k+1}^0{a^{k+1}}+C_{k+1}^1{a^k}b+…+C_{k+1}^r{a^{k+1-r}}{b^r}+…+C_{k+1}^ka{b^k}+C_{k+1}^{k+1}{b^{k+1}}$=(a+b)k+1
所以,结论对n=k+1时也成立.
由①②得,原命题得证.
点评 本题考查了数学归纳法及其组合数的运算性质、二项式定理,考查了推理能力与计算能力,属于中档题.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:解答题
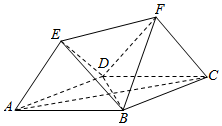 如图,多面体ABCDEF中,四边形ABCD为菱形,且∠DAB=60°,EF∥AC,AD=2,EA=ED=EF=$\sqrt{3}$.
如图,多面体ABCDEF中,四边形ABCD为菱形,且∠DAB=60°,EF∥AC,AD=2,EA=ED=EF=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 40 | B. | 50 | C. | 60 | D. | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
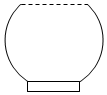 一个高为H容积为V的鱼缸的轴截面如图所示.现向空鱼缸内注水,直到注满为止.当鱼缸水深为h时,水的体积记为v.函数v=f(h)的大致图象可能是( )
一个高为H容积为V的鱼缸的轴截面如图所示.现向空鱼缸内注水,直到注满为止.当鱼缸水深为h时,水的体积记为v.函数v=f(h)的大致图象可能是( )| A. | 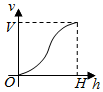 | B. | 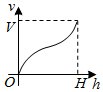 | C. | 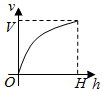 | D. | 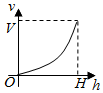 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com