
分析 (1)可分两步求解,先选出四人,再作一全排列计算出不同的选法种数;
(2)可分两步求解,先选出四人,再作一全排列计算出不同的选法种数,由于“男、女同学分别至少有1名”包括了三个事件,“一男三女”,“二男二女”,“三男一女”,选人时要分三类计数,然后再进行全排列;
(3)可计算出男同学甲与女同学乙同时选出的情况种数,从(2)的结果中排除掉,即可得到事件“在(2)的前提下,男同学甲与女同学乙不能同时选出”的选法种数
解答 解:(1)男、女同学各2名的选法有C42×C52=6×10=60种,故总的不同选法有60×A44=1440种;
即男女同学各两名的选法共有1440种.
(2)“男、女同学分别至少有1名”包括有“一男三女”,“二男二女”,“三男一女”,故选人种数为C41×C53+C42×C52+C43×C51=40+60+20=120
故总的安排方法有120×A44=2880
故不同的选法有2880种.
(3)可计算男同学甲与女同学乙同时选出的种数,由于已有两人,故再选两人即可,此两人可能是两男,一男一女,两女,故总的选法有C32+C41×C31+C42=21
故总的选法有2880-21×A44=2376
故不同的选法种数是2376种
点评 本题考查排列、组合及简单计数问题,解题的关键是正确理解题设中的事件,及理解计数原理,本题考查了分类的及运算的能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\sqrt{5}$ | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
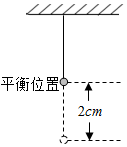 如图所示,一个小球做简谐运动,当时间t=0s时,小球在平衡位置,当t=1s时,小球第一次达到偏离平衡位置最大距离,这时小球离开平衡位置2cm,若该简谐运动的解析式为y=Asin(ωt+φ),则A,ω,φ的值分别是多少?
如图所示,一个小球做简谐运动,当时间t=0s时,小球在平衡位置,当t=1s时,小球第一次达到偏离平衡位置最大距离,这时小球离开平衡位置2cm,若该简谐运动的解析式为y=Asin(ωt+φ),则A,ω,φ的值分别是多少?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 经过圆外一点与圆相切的直线至多有两条 | |
| B. | 经过圆外一点与圆相切的直线有两条 | |
| C. | 经过圆外一点与圆相切的直线不存在 | |
| D. | 经过圆外一点与圆相切的直线至多有一条 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com