
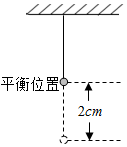
 如图所示,一个小球做简谐运动,当时间t=0s时,小球在平衡位置,当t=1s时,小球第一次达到偏离平衡位置最大距离,这时小球离开平衡位置2cm,若该简谐运动的解析式为y=Asin(ωt+φ),则A,ω,φ的值分别是多少?
如图所示,一个小球做简谐运动,当时间t=0s时,小球在平衡位置,当t=1s时,小球第一次达到偏离平衡位置最大距离,这时小球离开平衡位置2cm,若该简谐运动的解析式为y=Asin(ωt+φ),则A,ω,φ的值分别是多少? 科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{4}$ | B. | $\frac{6}{5}$ | C. | $\frac{5}{3}$ | D. | $\frac{8}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
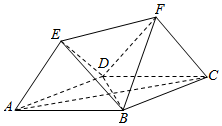 如图,多面体ABCDEF中,四边形ABCD为菱形,且∠DAB=60°,EF∥AC,AD=2,EA=ED=EF=$\sqrt{3}$.
如图,多面体ABCDEF中,四边形ABCD为菱形,且∠DAB=60°,EF∥AC,AD=2,EA=ED=EF=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{3}+1}{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | $\frac{1}{3}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
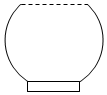 一个高为H容积为V的鱼缸的轴截面如图所示.现向空鱼缸内注水,直到注满为止.当鱼缸水深为h时,水的体积记为v.函数v=f(h)的大致图象可能是( )
一个高为H容积为V的鱼缸的轴截面如图所示.现向空鱼缸内注水,直到注满为止.当鱼缸水深为h时,水的体积记为v.函数v=f(h)的大致图象可能是( )| A. | 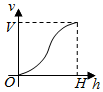 | B. | 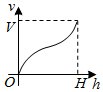 | C. | 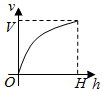 | D. | 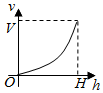 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com