
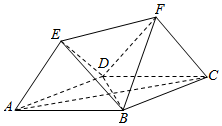
 如图,多面体ABCDEF中,四边形ABCD为菱形,且∠DAB=60°,EF∥AC,AD=2,EA=ED=EF=$\sqrt{3}$.
如图,多面体ABCDEF中,四边形ABCD为菱形,且∠DAB=60°,EF∥AC,AD=2,EA=ED=EF=$\sqrt{3}$.分析 解法一:(Ⅰ)取AD中点O,连结EO,BO.证明EO⊥AD.BO⊥AD.说明AD⊥平面BEO,即可证明AD⊥BE.
(Ⅱ)证明EO⊥OB,然后证明EO⊥平面ABCD.通过VF-BCD=VE-BCD求解即可.
解法二:(Ⅰ)同解法一.
(Ⅱ)证明EO⊥OB,利用AD⊥平面EOB,以及VF-BCD=VE-BCD=VE-ABD求解即可.
解答 解法一:(Ⅰ)如图,取AD中点O,连结EO,BO.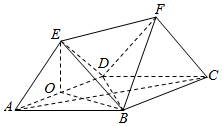
∵EA=ED,∴EO⊥AD.…(1分)
∵四边形ABCD为菱形,
∴AB=AD,
又∠DAB=60°,∴△ABD为等边三角形,∴BA=BD,
∴BO⊥AD.(3分)
∵BO∩EO=O,BO?平面BEO,EO?平面BEO,∴AD⊥平面BEO,(5分)
∵BE?平面BEO,∴AD⊥BE.(6分)
(Ⅱ)在△EAD中,$EA=ED=\sqrt{3}$,AD=2,
∴$EO=\sqrt{A{E^2}-A{O^2}}=\sqrt{2}$,
∵△ABD为等边三角形,∴AB=BD=AD=2,∴$BO=\sqrt{3}$.(7分)
又 $BE=\sqrt{5}$,∴EO2+OB2=BE2,∴EO⊥OB,(8分)
∵AD∩OB=O,AD?平面ABCD,BO?平面ABCD,
∴EO⊥平面ABCD.(9分)
又${S_{△ABD}}=\frac{1}{2}•AD•OB=\frac{1}{2}×2×\sqrt{3}=\sqrt{3}$,(10分)
∴${S_{△BCD}}={S_{△ABD}}=\sqrt{3}$.
又∵EF∥AC,
∴VF-BCD=VE-BCD(11分)=$\frac{1}{3}{S_{△BCD}}•EO=\frac{1}{3}×\sqrt{3}×\sqrt{2}=\frac{{\sqrt{6}}}{3}$.(12分)
解法二:(Ⅰ)同解法一.(6分)
(Ⅱ)在△EAD中,$EA=ED=\sqrt{3}$,AD=2,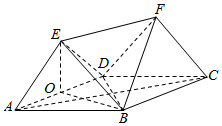
∴$EO=\sqrt{A{E^2}-A{O^2}}=\sqrt{2}$,
∵△ABD为等边三角形,
∴AB=BD=AD=2,∴$BO=\sqrt{3}$.(7分)
又 $BE=\sqrt{5}$,∴EO2+OB2=BE2,∴EO⊥OB,(8分)
所以${S_{△EOB}}=\frac{1}{2}•EO•OB=\frac{1}{2}×\sqrt{2}×\sqrt{3}=\frac{{\sqrt{6}}}{2}$.(9分)
又S△BCD=S△ABD,EF∥AC,AD⊥平面EOB,
∴VF-BCD=VE-BCD=VE-ABD(10分)=$\frac{1}{3}{S_{△EOB}}•AD=\frac{1}{3}×\frac{{\sqrt{6}}}{2}×2=\frac{{\sqrt{6}}}{3}$.(12分)
点评 本题主要考查空间直线与直线、直线与平面的位置关系及几何体的体积等基础知识,考查空间想象能力、推理论证能力、运算求解能力,考查化归与转化思想等.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{4}$-y2=1 | C. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{2}$=1 | D. | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{3}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{5}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\sqrt{5}$ | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠DAB是直角,AB∥CD,AD=CD=2AB=2,E、F分别为PC、CD的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠DAB是直角,AB∥CD,AD=CD=2AB=2,E、F分别为PC、CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x1+x2+x3>0 | B. | x1+x2+x3<0 | C. | f(x1+x2+x3)≥0 | D. | f(x1+x2+x3)≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
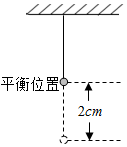 如图所示,一个小球做简谐运动,当时间t=0s时,小球在平衡位置,当t=1s时,小球第一次达到偏离平衡位置最大距离,这时小球离开平衡位置2cm,若该简谐运动的解析式为y=Asin(ωt+φ),则A,ω,φ的值分别是多少?
如图所示,一个小球做简谐运动,当时间t=0s时,小球在平衡位置,当t=1s时,小球第一次达到偏离平衡位置最大距离,这时小球离开平衡位置2cm,若该简谐运动的解析式为y=Asin(ωt+φ),则A,ω,φ的值分别是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com