
| A. | x1+x2+x3>0 | B. | x1+x2+x3<0 | C. | f(x1+x2+x3)≥0 | D. | f(x1+x2+x3)≤0 |
分析 由函数的导函数得知在x∈(0,$\frac{π}{2}$)是单调递增的,再由奇偶性得到在x∈(-$\frac{π}{2}$,$\frac{π}{2}$)上单调递增,通过单调性与奇偶性相结合得到x1+x2+x3≥0,所以对应的函数值可以确定.
解答 解:∵函数f(x)=$\frac{x}{cosx}$的定义域为(-$\frac{π}{2}$,$\frac{π}{2}$),且f(-x)=-f(x)
∴f(x)为奇函数
∵f′(x)=$\frac{cosx+xsinx}{(cosx)^{2}}$
∴f(x)在x∈(0,$\frac{π}{2}$)是单调递增的.
∴f(x)在x∈(-$\frac{π}{2}$,$\frac{π}{2}$)上单调递增.
∵f(x1)+f(x2)≥0,
∴f(x1)≥-f(x2)≥0,
∴f(x1)≥f(-x2)≥0,
∴x1≥-x2,
同理可得:x2≥-x3,x3≥-x1
∴x1+x2≥0,x2+x3≥0,x3+x1≥0
∴x1+x2+x3≥0,
∴f(x1+x2+x3)≥f(0)=0,
故选C
点评 本题考查由函数的导函数和奇偶性得到单调性,从而得到x1+x2+x3≥0,所以对应的函数值可以确定.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:解答题
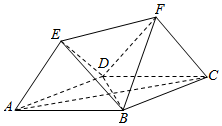 如图,多面体ABCDEF中,四边形ABCD为菱形,且∠DAB=60°,EF∥AC,AD=2,EA=ED=EF=$\sqrt{3}$.
如图,多面体ABCDEF中,四边形ABCD为菱形,且∠DAB=60°,EF∥AC,AD=2,EA=ED=EF=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4x±3y=0 | B. | 3x±4y=0 | C. | 16x±9y=0 | D. | 9x±16y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{3}+1}{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | $\frac{1}{3}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com