
分析 函数y=g(x)恰有3个零点,可化为函数y=f(2-x)与y=b的图象有3个交点,从而化简y=f(2-x),作图象求解.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{2-|x|,x≤2}\\{(x-2)^{2},x>2}\end{array}\right.$,
∴f(2-x)=$\left\{\begin{array}{l}{2-|2-x|,x≥0}\\{{x}^{2},x<0}\end{array}\right.$,
∵函数g(x)=b-f(2-x),其中b∈R,若函数y=g(x)恰有3个零点,
∴方程b-f(2-x)=0有3个解,
即函数y=f(2-x)与y=b的图象有3个交点,
y=f(2-x)=$\left\{\begin{array}{l}{4-x,x>2}\\{x,0≤x≤2}\\{{x}^{2},x<0}\end{array}\right.$,
作函数y=f(2-x)与y=b的图象如下,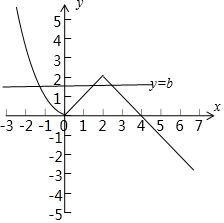
结合图象可知,
0<b<2,
故答案为:(0,2).
点评 本题考查了分段函数的应用及数形结合的思想应用,同时考查了函数的零点与函数的图象的交点的关系应用.


 互动英语系列答案
互动英语系列答案科目:高中数学 来源: 题型:填空题
 已知如图几何体,正方形ABCD和矩形ABEF所在平面互相垂直,AF=2AB=2AD=2,M为AF的中点,BN⊥CE,垂足为N.
已知如图几何体,正方形ABCD和矩形ABEF所在平面互相垂直,AF=2AB=2AD=2,M为AF的中点,BN⊥CE,垂足为N.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 优秀 | 非优秀 | 总计 | |
| 甲班 | 10 | ||
| 乙班 | 30 | ||
| 合计 |
| P(K2≥x0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| x0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{2}$,+∞) | B. | (-∞,$\frac{1}{2}$]∪[3,+∞) | C. | (-∞,0]∪[$\frac{1}{2}$,3) | D. | [$\frac{1}{2}$,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-13,-1] | B. | (-∞,-1] | C. | [-13,+∞) | D. | [1,13] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-2≤x≤2} | B. | {x|-2≤x≤4} | C. | {x|0<x≤2} | D. | {x|2≤x≤4} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com