
【题目】命题![]() :指数函数
:指数函数![]() 是减函数;命题
是减函数;命题![]() :
:![]() ,使关于
,使关于![]() 的方程
的方程![]() 有实数解,其中
有实数解,其中![]() .
.
(1)当![]() 时,若
时,若![]() 为真命题,求
为真命题,求![]() 的取值范围;
的取值范围;
(2)当![]() 时,若
时,若![]() 且
且![]() 为假命题,求
为假命题,求![]() 的取值范围.
的取值范围.
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:
【题目】已知中心在坐标原点的椭圆与双曲线有公共焦点,且左、右焦点分别为![]() ,
,![]() .这两条曲线在第一象限的交点为
.这两条曲线在第一象限的交点为![]() ,
,![]() 是以
是以![]() 为底边的等腰三角形.若
为底边的等腰三角形.若![]() ,记椭圆与双曲线的离心率分别为
,记椭圆与双曲线的离心率分别为![]() 、
、![]() ,则
,则![]() 的取值范围是_____.
的取值范围是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市2011年至2017年新开楼盘的平均销售价格(单位:千元/平方米)的统计数据如下表:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售价格 | 3 | 3.4 | 3.7 | 4.5 | 4.9 | 5.3 | 6 |
(1)求![]() 关于x的线性回归方程;
关于x的线性回归方程;
(2)利用(1)中的回归方程,分析2011年至2017年该市新开楼盘平均销售价格的变化情况,并预测该市2019年新开楼盘的平均销售价格。
附:参考公式: 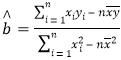 ,
,![]() ,其中
,其中![]() 为样本平均值。
为样本平均值。
参考数据:![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,左顶点B与右焦点
,左顶点B与右焦点![]() 之间的距离为3.
之间的距离为3.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)设直线![]() 交
交![]() 轴于点
轴于点![]() ,过
,过![]() 且斜率不为
且斜率不为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于两点
相交于两点![]() ,连接
,连接![]() 并延长分别与直线
并延长分别与直线![]() 交于两点
交于两点![]() . 若
. 若![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log4(4x+1)+kx(k∈R)是偶函数.
(1)求k的值;
(2)设g(x)=log4![]() ,若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
,若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在(0,+∞)上的函数f(x),对于任意的m,n∈(0,+∞),都有f(mn)=f(m)+f(n)成立,当x>1时,f(x)<0.
(1)求证:1是函数f(x)的零点;
(2)求证:f(x)是(0,+∞)上的减函数;
(3)当f(2)=![]() 时,解不等式f(ax+4)>1.
时,解不等式f(ax+4)>1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某食品厂生产的面包中抽取![]() 个,测量这些面包的一项质量指标值,由测量结果得如下频数分布表:
个,测量这些面包的一项质量指标值,由测量结果得如下频数分布表:
质量指标值分组 |
|
|
|
|
|
频数 |
|
|
|
|
|

(1)在相应位置上作出这些数据的频率分布直方图;
(2)估计这种面包质量指标值的平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(3)根据以上抽样调查数据,能否认为该食品厂生产的这种面包符合“质量指标值不低于![]() 的面包至少要占全部面包
的面包至少要占全部面包![]() 的规定?”
的规定?”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com