
【题目】设数列![]() 的前n项和为
的前n项和为![]() ,已知
,已知![]() ,
,![]() ,
,![]() .
.
(1)证明:![]() 为等比数列,求出
为等比数列,求出![]() 的通项公式;
的通项公式;
(2)若![]() ,求
,求![]() 的前n项和
的前n项和![]() ,并判断是否存在正整数n使得
,并判断是否存在正整数n使得![]() 成立?若存在求出所有n值;若不存在说明理由.
成立?若存在求出所有n值;若不存在说明理由.
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】某人某天的工作是驾车从![]() 地出发,到
地出发,到![]() 两地办事,最后返回
两地办事,最后返回![]() 地,
地,![]() ,三地之间各路段行驶时间及拥堵概率如下表
,三地之间各路段行驶时间及拥堵概率如下表
路段 | 正常行驶所用时间(小时) | 上午拥堵概率 | 下午拥堵概率 |
| 1 | 0.3 | 0.6 |
| 2 | 0.2 | 0.7 |
| 3 | 0.3 | 0.9 |
若在某路段遇到拥堵,则在该路段行驶时间需要延长1小时.
现有如下两个方案:
方案甲:上午从![]() 地出发到
地出发到![]() 地办事然后到达
地办事然后到达![]() 地,下午从
地,下午从![]() 地办事后返回
地办事后返回![]() 地;
地;
方案乙:上午从![]() 地出发到
地出发到![]() 地办事,下午从
地办事,下午从![]() 地出发到达
地出发到达![]() 地,办完事后返回
地,办完事后返回![]() 地.
地.
(1)若此人早上8点从![]() 地出发,在各地办事及午餐的累积时间为2小时,且采用方案甲,求他当日18点或18点之前能返回
地出发,在各地办事及午餐的累积时间为2小时,且采用方案甲,求他当日18点或18点之前能返回![]() 地的概率.
地的概率.
(2)甲乙两个方案中,哪个方案有利于办完事后更早返回![]() 地?请说明理由.
地?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称.某市为了了解人们对“一带一路”的认知程度,对不同年龄和不同职业的人举办了一次“一带一路”知识竞赛,满分100分(90分及以上为认知程度高).现从参赛者中抽取了![]() 人,按年龄分成5组,第一组:
人,按年龄分成5组,第一组: ![]() ,第二组:
,第二组: ![]() ,第三组:
,第三组: ![]() ,第四组:
,第四组: ![]() ,第五组:
,第五组: ![]() ,得到如图所示的频率分布直方图,已知第一组有6人.
,得到如图所示的频率分布直方图,已知第一组有6人.
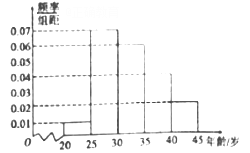
(1)求![]() ;
;
(2)求抽取的![]() 人的年龄的中位数(结果保留整数);
人的年龄的中位数(结果保留整数);
(3)从该市大学生、军人、医务人员、工人、个体户 五种人中用分层抽样的方法依次抽取6人,42人,36人,24人,12人,分别记为1~5组,从这5个按年龄分的组和5个按职业分的组中每组各选派1人参加知识竞赛,分别代表相应组的成绩,年龄组中1~5组的成绩分别为93,96,97,94,90,职业组中1~5组的成绩分别为93,98,94,95,90.
(Ⅰ)分别求5个年龄组和5个职业组成绩的平均数和方差;
(Ⅱ)以上述数据为依据,评价5个年龄组和5个职业组对“一带一路”的认知程度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要得到![]() 的图象
的图象![]() ,只要将
,只要将![]() 图象
图象![]() 怎样变化得到( )
怎样变化得到( )
A.将![]() 的图象
的图象![]() 沿x轴方向向左平移
沿x轴方向向左平移![]() 个单位
个单位
B.将![]() 的图象
的图象![]() 沿x轴方向向右平移
沿x轴方向向右平移![]() 个单位
个单位
C.先作![]() 关于x轴对称图象
关于x轴对称图象![]() ,再将图象
,再将图象![]() 沿x轴方向向右平移
沿x轴方向向右平移![]() 个单位
个单位
D.先作![]() 关于x轴对称图象
关于x轴对称图象![]() ,再将图象
,再将图象![]() 沿x轴方向向左平移
沿x轴方向向左平移![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学名著,它在几何学中的研究比西方早1000多年,在《九章算术》中,将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵(qian du);阳马指底面为矩形,一侧棱垂直于底面的四棱锥,鳖膈(bie nao)指四个面均为直角三角形的四面体.如图在堑堵![]() 中,
中,![]() .
.
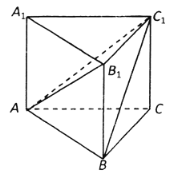
(1)求证:四棱锥![]() 为阳马;
为阳马;
(2)若![]() ,当鳖膈
,当鳖膈![]() 体积最大时,求锐二面角
体积最大时,求锐二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,O为坐标原点,点F为抛物线C1:![]() 的焦点,且抛物线C1上点P处的切线与圆C2:
的焦点,且抛物线C1上点P处的切线与圆C2:![]() 相切于点Q.
相切于点Q.

(Ⅰ)当直线PQ的方程为![]() 时,求 抛物线C1的方程;
时,求 抛物线C1的方程;
(Ⅱ)当正数P变化时,记S1 ,S2分别为△FPQ,△FOQ的面积,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点![]() ,动点
,动点![]() 与
与![]() 、
、![]() 两点连线的斜率之积为
两点连线的斜率之积为![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)已知点![]() 是轨迹
是轨迹![]() 上的动点,点
上的动点,点![]() 在直线
在直线![]() 上,且满足
上,且满足![]() (其中
(其中![]() 为坐标原点),求
为坐标原点),求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com