
ЗжЮі ЃЈIЃЉРћгУЕШВюЪ§СаЕФЭЈЯюЙЋЪНПЩЕУanЃЌРћгУЪ§СаЕнЭЦЙиЯЕгыЕШБШЪ§СаЕФЭЈЯюЙЋЪНМДПЩЕУГіЃЎ
ЃЈIIЃЉРћгУЁАДэЮЛЯрМѕЗЈЁБгыЕШБШЪ§СаЕФЧѓКЭЙЋЪНМДПЩЕУГіЃЎ
НтД№ ЃЈЂёЃЉжЄУїЃКЩшЕШВюЪ§Са{an}ЕФЙЋВюЮЊdЃЌЁпa1=1ЃЌa5=9ЃЌЁр9=1+4dЃЌНтЕУd=2ЃЎ
Ёрan=1+2ЃЈn-1ЃЉ=2n-1ЃЎ
Ъ§Са{an}ЁЂ{bn}Тњзу$\frac{{a}_{1}}{{b}_{1}}$+$\frac{{a}_{2}}{{b}_{2}}$+$\frac{{a}_{3}}{{b}_{3}}$+Ё+$\frac{{a}_{n}}{{b}_{n}}$=6-$\frac{{a}_{n+2}}{{b}_{n}}$ЃЈnЁЪN*ЃЉЃЎ
Ёрn=1ЪБЃЌ$\frac{{a}_{1}}{{b}_{1}}$=6-$\frac{{a}_{3}}{{b}_{1}}$ЃЌПЩЕУ$\frac{1}{{b}_{1}}$=6-$\frac{5}{{b}_{1}}$ЃЌНтЕУb1=1ЃЎ
nЁн2ЪБЃЌ$\frac{{a}_{1}}{{b}_{1}}$+$\frac{{a}_{2}}{{b}_{2}}$+$\frac{{a}_{3}}{{b}_{3}}$+Ё+$\frac{{a}_{n-1}}{{b}_{n-1}}$=6-$\frac{{a}_{n+1}}{{b}_{n-1}}$ЃЈnЁЪN*ЃЉЃЎ
Ёр$\frac{{a}_{n}}{{b}_{n}}$=$\frac{{a}_{n+1}}{{b}_{n-1}}$-$\frac{{a}_{n+2}}{{b}_{n}}$ЃЌМД$\frac{2{a}_{n+1}}{{b}_{n}}$=$\frac{{a}_{n+1}}{{b}_{n-1}}$ЃЌЁр$\frac{{b}_{n}}{{b}_{n-1}}$=2ЃЎ
Ёр{bn}ЪЧвд1ЮЊЪзЯюЃЌ2ЮЊЙЋБШЕФЕШБШЪ§СаЃЎ
ЃЈЂђЃЉгЩЃЈIЃЉПЩЕУЃКbn=2n-1ЃЎ
Ёр$\frac{2+{a}_{n}}{{b}_{n}}$=$\frac{2n+1}{{2}^{n-1}}$ЃЌ
Ъ§Са{$\frac{2+{a}_{n}}{{b}_{n}}$}ЕФЧАnЯюЕФКЭSn=3ЁС1+5ЁС$\frac{1}{2}$+7ЁС$ЃЈ\frac{1}{2}ЃЉ^{2}$+Ё+ЃЈ2n+1ЃЉЁС$ЃЈ\frac{1}{2}ЃЉ^{n-1}$ЃЌ
Ёр$\frac{1}{2}{S}_{n}$=$3ЁС\frac{1}{2}$+5ЁС$ЃЈ\frac{1}{2}ЃЉ^{2}$+Ё+ЃЈ2n-1ЃЉЁС$ЃЈ\frac{1}{2}ЃЉ^{n-1}$+ЃЈ2n+1ЃЉЁС$ЃЈ\frac{1}{2}ЃЉ^{n}$ЃЌ
$\frac{1}{2}{S}_{n}$=3+2$[\frac{1}{2}+ЃЈ\frac{1}{2}ЃЉ^{2}+ЁЃЈ\frac{1}{2}ЃЉ^{n-1}]$-ЃЈ2n+1ЃЉЁС$ЃЈ\frac{1}{2}ЃЉ^{n}$=3+2ЁС$\frac{\frac{1}{2}ЃЈ1-\frac{1}{{2}^{n-1}}ЃЉ}{1-\frac{1}{2}}$-ЃЈ2n+1ЃЉЁС$ЃЈ\frac{1}{2}ЃЉ^{n}$ЃЌ
ЁрSn=10-$\frac{2n+5}{{2}^{n-1}}$ЃЎ
ЕуЦР БОЬтПМВщСЫЁАДэЮЛЯрМѕЗЈЁБЁЂЕШВюЪ§СагыЕШБШЪ§СаЕФЭЈЯюЙЋЪНгыЧѓКЭЙЋЪНЃЌПМВщСЫЭЦРэФмСІгыМЦЫуФмСІЃЌЪєгкжаЕЕЬтЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | $-\sqrt{2}$ | BЃЎ | $\frac{{\sqrt{2}}}{2}$ | CЃЎ | 1 | DЃЎ | $\sqrt{2}$ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 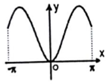 | BЃЎ | 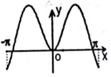 | CЃЎ | 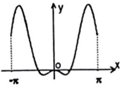 | DЃЎ | 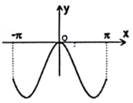 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | -1 | BЃЎ | 1 | CЃЎ | 2 | DЃЎ | -2 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
 ХзЮяЯпy=x2ЃЈ-2ЁмxЁм2ЃЉШЦyжса§зЊвЛжмаЮГЩвЛИіШчЭМЫљЪОЕФХзЮяУцЮЇГЩЕФМИКЮЬхЃЌдкДЫа§зЊЬхФкЫЎЦНЗХШывЛИіе§ЗНЬхЃЌЪЙе§ЗНЬхЕФвЛИіУцЧЁКУгыа§зЊЬхЕФПЊПкУцЦНЦыЃЌдђДЫе§ЗНЬхЕФРтГЄЪЧЃЈЁЁЁЁЃЉ
ХзЮяЯпy=x2ЃЈ-2ЁмxЁм2ЃЉШЦyжса§зЊвЛжмаЮГЩвЛИіШчЭМЫљЪОЕФХзЮяУцЮЇГЩЕФМИКЮЬхЃЌдкДЫа§зЊЬхФкЫЎЦНЗХШывЛИіе§ЗНЬхЃЌЪЙе§ЗНЬхЕФвЛИіУцЧЁКУгыа§зЊЬхЕФПЊПкУцЦНЦыЃЌдђДЫе§ЗНЬхЕФРтГЄЪЧЃЈЁЁЁЁЃЉ| AЃЎ | 1 | BЃЎ | 2 | CЃЎ | $\sqrt{2}$ | DЃЎ | 4 |
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com