
| A. | -2 | B. | -1 | C. | 2 | D. | 1 |
分析 先画出满足条件$\left\{\begin{array}{l}{y≥0\\;}\\{x-y≥1}\\{x+2y≤4}\end{array}\right.$表示的平面区域,再根据x+sy+t≥0表示的平面区域表示为直线x+sy+t=0右侧的阴影部分,结合已知中不等式组$\left\{\begin{array}{l}{y≥0}\\{x-y≥1}\\{x+2y≤4}\\{x+sy+t≥0}\end{array}\right.$所表示的平面区域是面积为1的直角三角形,得到满足条件的直线,进而根据直线的方程求出t的值.
解答  解:满足条件$\left\{\begin{array}{l}{y≥0\\;}\\{x-y≥1}\\{x+2y≤4}\end{array}\right.$,的平面区域如下图所示:
解:满足条件$\left\{\begin{array}{l}{y≥0\\;}\\{x-y≥1}\\{x+2y≤4}\end{array}\right.$,的平面区域如下图所示:
由于x+sy+t≥0表示的平面区域表示为直线x+sy+t=0右侧的阴影部分面积,
故分析可得直线x+sy+t=0有2种情况:
①过(2,1)点且与直线直线x+2y=4垂直,解得t=-$\frac{3}{2}$,但由于直角三角形面积为1,不满足题意,故舍去.
②过(2,1)点且与x轴垂直,t=-2,满足直角三角形的面积为1,满足题意;
故选:A.
点评 本题考查的知识点是二元一次不等式(组)与平面区域,根据已知条件分析满足的直线方程是解答本题的关键.


科目:高中数学 来源: 题型:选择题

| A. | $\frac{n(3n-1)}{2}$ | B. | $\frac{(3n+2)(n+1)}{2}$ | C. | $\frac{(3n-2)(n+1)}{2}$ | D. | $\frac{(3n+2)(n-1)}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1] | B. | [1,2] | C. | [0,2] | D. | [0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
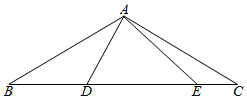 如图,在三角形ABC中,∠BAC=120°,AB=AC=2,D,E为BC边上的点,且$\overrightarrow{BC}$=3$\overrightarrow{BD}$=2$\overrightarrow{DE}$,则$\overrightarrow{AD}$•$\overrightarrow{AE}$=$\frac{1}{3}$.
如图,在三角形ABC中,∠BAC=120°,AB=AC=2,D,E为BC边上的点,且$\overrightarrow{BC}$=3$\overrightarrow{BD}$=2$\overrightarrow{DE}$,则$\overrightarrow{AD}$•$\overrightarrow{AE}$=$\frac{1}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com