
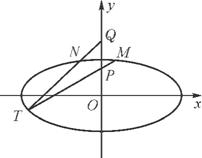
如图,在平面直角坐标系xOy中,椭圆C: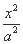 +
+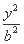 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为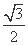 ,以原点为圆心、椭圆C的短半轴长为半径的圆与直线x-y+2=0相切.
,以原点为圆心、椭圆C的短半轴长为半径的圆与直线x-y+2=0相切.
(1) 求椭圆C的方程;
(2) 已知点P(0,1),Q(0,2),设M,N是椭圆C上关于y轴对称的不同两点,直线PM与QN相交于点T,求证:点T在椭圆C上.
(1) 由题意知b=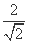 =
= .
.
因为离心率e= =
=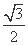 ,
,
所以 =
= =
=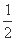 .
.
所以a=2 .
.
所以椭圆C的方程为 +
+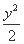 =1.
=1.
(2) 由题意可设M,N的坐标分别为(x0,y0),(-x0,y0),则
直线PM的方程为y= x+1 ①,
x+1 ①,
直线QN的方程为y=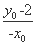 x+2 ②.
x+2 ②.
方法一 联立①②解得x= ,y=
,y=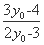 ,
,
即T .
.
由 +
+ =1,可得
=1,可得 =8-4
=8-4 .
.
因为 +
+ =
= =
= =
=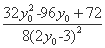 =
= =1,
=1,
所以点T坐标满足椭圆C的方程,即点T在椭圆C上.
方法二 设T(x,y).
联立①②解得x0= ,y0=
,y0=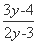 .
.
因为 +
+ =1,所以
=1,所以 +
+ =1,
=1,
整理得 +
+ =(2y-3)2,
=(2y-3)2,
所以 +
+ -12y+8=4y2-12y+9,
-12y+8=4y2-12y+9,
即 +
+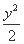 =1.
=1.
所以点T坐标满足椭圆C的方程,即点T在椭圆C上.


科目:高中数学 来源: 题型:
在平面直角坐标系xOy中,过椭圆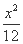 +
+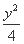 =1在第一象限内的一点P(x,y)分别作x轴、y轴的两条垂线,垂足分别为M,N,求矩形PMON的周长最大值时点P的坐标.
=1在第一象限内的一点P(x,y)分别作x轴、y轴的两条垂线,垂足分别为M,N,求矩形PMON的周长最大值时点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知( +x2
+x2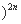 的展开式的二项式系数和比(3x-1)n的展开式的二项式系数和大992.
的展开式的二项式系数和比(3x-1)n的展开式的二项式系数和大992.
(1) 求 的展开式中二项式系数最大的项;
的展开式中二项式系数最大的项;
(2) 求 的展开式中系数的绝对值最大的项.
的展开式中系数的绝对值最大的项.
查看答案和解析>>
科目:高中数学 来源: 题型:
阅读下面的四段话,其中不是解决问题的算法的是( )
A.求1×2×3的值,先计算1×2=2,再计算2×3=6,最终结果为6
B.解一元一次方程的步骤是去分母、去括号、移项、合并同类项、系数化为1
C.今天,我上了8节课,真累
D.求1+2+3+4+5的值,先计算1+2=3,再计算3+3=6,6+4=10,10+5=15,最终结果为15
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com