
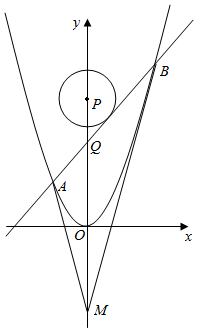
 已知抛物线C:x2=y,圆C2,半径为1,圆心P(0,t)t>1,且t为常数,Q为y轴非负半轴上异于P的点,过Q作圆C2切线,交抛物线于A、B两点.
已知抛物线C:x2=y,圆C2,半径为1,圆心P(0,t)t>1,且t为常数,Q为y轴非负半轴上异于P的点,过Q作圆C2切线,交抛物线于A、B两点.分析 (1)直接利用抛物线的方程,可得抛物线焦点与准线方程;
(2)若M是Q点关于原点的对称点.
(i)证明kMA=-kMB,可得直线MA、MB关于y轴对称;
(ii)求出$\frac{2S}{|MQ|}$,即可求$\frac{2S}{|MQ|}$的最小值.
解答 解:(1)∵抛物线C:x2=y,
∴抛物线焦点为(0,$\frac{1}{4}$),准线方程为y=-$\frac{1}{4}$;
(2)(i)设A(x1,y1),B(x2,y2),直线AB的方程为y=kx+a,代入x2=y,可得x2-kx-a=0,
∴x1+x2=k,x1x2=-a,
∴kMA+kMB=$\frac{{y}_{1}+a}{{x}_{1}}$+$\frac{{y}_{2}+a}{{x}_{2}}$=2k+2a•$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=2k+2a•$\frac{k}{-a}$=0,
∴kMA=-kMB,
∴直线MA、MB关于y轴对称;
(ii)∵AB与圆相切,
∴$\frac{|a-t|}{\sqrt{{k}^{2}+1}}$=1,
∴k2=(a-t)2-1,
$\frac{2S}{|MQ|}$=$\frac{2×\frac{1}{2}×2a×|{x}_{1}-{x}_{2}|}{2a}$=|x1-x2|=k2+4a=(a-t)2-1+4a=a2+(4-2t)a+t2-1=(a+2-t)2+4t-5,
∵k2=(a-t)2-1>0,∴a>t+1或a<t-1,
∴a=t-2时,$\frac{2S}{|MQ|}$取得最小值4t-5.
点评 本题考查抛物线的方程与性质,考查直线与圆、抛物线的位置关系,考查学生分析解决问题的能力,属于中档题.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -2-$\sqrt{2}$ | C. | 2$\sqrt{2}$-3 | D. | 8-6$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | 8 | C. | $\frac{1}{2}$ | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com