
分析 由题意可得:$\frac{p}{2}$=c,-$\frac{2{a}^{2}}{c}$=-$\frac{p}{2}$,又a2+b2=c2,联立解出即可得出.
解答 解:由题意可得:$\frac{p}{2}$=c,-$\frac{2{a}^{2}}{c}$=-$\frac{p}{2}$,又a2+b2=c2,联立解得c=$\frac{p}{2}$,a=$\frac{\sqrt{2}}{4}$p,b=$\frac{\sqrt{2}}{4}p$.
∴$\frac{b}{a}$=1.
∴双曲线的渐近线方程为:y=±x.
故答案为:y=±x.
点评 本题考查了抛物线与双曲线的标准方程及其性质,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{2}$ | B. | ±$\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | $±\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某几何体的三视图如图所示,其中正视图是腰长为2的等腰三角形,俯视图是半径为1的半圆,则该几何体的侧面积是( )
某几何体的三视图如图所示,其中正视图是腰长为2的等腰三角形,俯视图是半径为1的半圆,则该几何体的侧面积是( )| A. | $\sqrt{3}$ | B. | π | C. | $2π+\sqrt{3}$ | D. | $π+\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
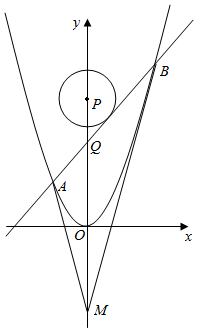 已知抛物线C:x2=y,圆C2,半径为1,圆心P(0,t)t>1,且t为常数,Q为y轴非负半轴上异于P的点,过Q作圆C2切线,交抛物线于A、B两点.
已知抛物线C:x2=y,圆C2,半径为1,圆心P(0,t)t>1,且t为常数,Q为y轴非负半轴上异于P的点,过Q作圆C2切线,交抛物线于A、B两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,某汽车前灯的反光曲面与轴截面的交线为抛物线的一部分,灯口直径AB为140$\sqrt{2}$mm,反光曲面的顶点O到灯口的距离是70mm,由抛物线的性质可知,当灯泡安装在抛物线的焦点处时,经反光曲面反射的光束是平行光束,问:为了获得平行光束,应怎样安装灯泡?
如图,某汽车前灯的反光曲面与轴截面的交线为抛物线的一部分,灯口直径AB为140$\sqrt{2}$mm,反光曲面的顶点O到灯口的距离是70mm,由抛物线的性质可知,当灯泡安装在抛物线的焦点处时,经反光曲面反射的光束是平行光束,问:为了获得平行光束,应怎样安装灯泡?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,已知抛物线C:y2=2px(p>0)的焦点是F,抛物线C上的横坐标为1的点到焦点F的距离是2,直线l经过点F交抛物线C于A、B两点,A点在x轴下方,点D和点A关于x轴对称.
如图所示,已知抛物线C:y2=2px(p>0)的焦点是F,抛物线C上的横坐标为1的点到焦点F的距离是2,直线l经过点F交抛物线C于A、B两点,A点在x轴下方,点D和点A关于x轴对称.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com