
分析 化抛物线方程为标准方程,求得p,进一步求得$\frac{p}{2}$,再由不同类型的标准方程求出对应的焦点坐标和准线方程.
解答 解:(1)由x2+6y=0,得x2=-6y,
∴2p=6,p=3,$\frac{p}{2}=\frac{3}{2}$,则抛物线的焦点坐标为F(0,$-\frac{3}{2}$),准线方程为:y=$\frac{3}{2}$;
(2)由6y2=x,得${y}^{2}=\frac{1}{6}x$,
∴2p=$\frac{1}{6}$,p=$\frac{1}{12}$,$\frac{p}{2}=\frac{1}{24}$,则抛物线的焦点坐标为F($\frac{1}{24},0$),准线方程为:x=-$\frac{1}{24}$;
(3)由y=$\frac{1}{4}$x2,得x2=4y,
∴2p=4,p=2,$\frac{p}{2}=1$,则抛物线的焦点坐标为F(0,1),准线方程为:x=-1.
点评 本题考查抛物线的标准方程,考查由抛物线方程求焦点坐标和准线方程,是基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{2}$m2 | B. | $\frac{3}{2}$m2 | C. | -6m2 | D. | 12m2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
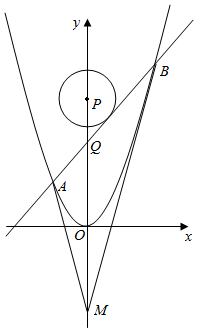 已知抛物线C:x2=y,圆C2,半径为1,圆心P(0,t)t>1,且t为常数,Q为y轴非负半轴上异于P的点,过Q作圆C2切线,交抛物线于A、B两点.
已知抛物线C:x2=y,圆C2,半径为1,圆心P(0,t)t>1,且t为常数,Q为y轴非负半轴上异于P的点,过Q作圆C2切线,交抛物线于A、B两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,某汽车前灯的反光曲面与轴截面的交线为抛物线的一部分,灯口直径AB为140$\sqrt{2}$mm,反光曲面的顶点O到灯口的距离是70mm,由抛物线的性质可知,当灯泡安装在抛物线的焦点处时,经反光曲面反射的光束是平行光束,问:为了获得平行光束,应怎样安装灯泡?
如图,某汽车前灯的反光曲面与轴截面的交线为抛物线的一部分,灯口直径AB为140$\sqrt{2}$mm,反光曲面的顶点O到灯口的距离是70mm,由抛物线的性质可知,当灯泡安装在抛物线的焦点处时,经反光曲面反射的光束是平行光束,问:为了获得平行光束,应怎样安装灯泡?查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
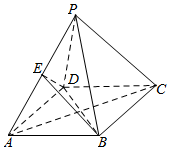 如图,正四棱锥P-ABCD中,底面ABCD的边长为4,PD=4,E为PA的中点,
如图,正四棱锥P-ABCD中,底面ABCD的边长为4,PD=4,E为PA的中点,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com