
分析 对a进行讨论,判断f(x)在(-∞,1)上的零点个数,再判断f(x)在[1,+∞)上的零点个数.
解答 解:当x<1时,f(x)在(-∞,1)上单调递增,f(x)<2+a,
当x≥1时,令f(x)=0得x=-a或x=-2a.
(1)若2+a≤0即a≤-2时,f(x)在(-∞,1)上无零点,
此时,-2a>-a≥2,∴f(x)在[1,+∞)上有两个零点,符合题意;
(2)若2+a>0即a>-2时,f(x)在(-∞,1)上有1个零点,
∴f(x)在[1,+∞)上只有1个零点,
①若-2<a<0,则-2a>-a,∴-a<1≤-2a,解得-1<a≤-$\frac{1}{2}$,
②若a=0,则-a=-2a=0∉[1,+∞),∴f(x)在[1,+∞)上无零点,不符合题意;
③若a>0,则0>-a>-2a,∴f(x)在[1,+∞)上无零点,不符合题意;
综上,a的取值范围是(-∞,-2]∪(-1,-$\frac{1}{2}$].
故答案为(-∞,-2]∪(-1,-$\frac{1}{2}$].
点评 本题考查了函数的零点个数与函数单调性的判断,分类讨论思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{4}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(x)=-f({x+\frac{π}{2}})$ | B. | $f(x)=f({-x+\frac{π}{2}})$ | C. | $f(x)•f({x+\frac{π}{2}})=1$ | D. | $f(x)=-f({-x+\frac{π}{2}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
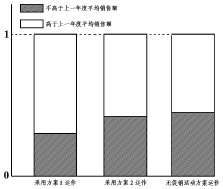 某公司为评估两套促销活动方案(方案1运作费用为5元/件;方案2的运作费用为2元/件),在某地区部分营销网点进行试点(每个试点网点只采用一种促销活动方案),运作一年后,对比该地区上一年度的销售情况,制作相应的等高条形图如图所示.
某公司为评估两套促销活动方案(方案1运作费用为5元/件;方案2的运作费用为2元/件),在某地区部分营销网点进行试点(每个试点网点只采用一种促销活动方案),运作一年后,对比该地区上一年度的销售情况,制作相应的等高条形图如图所示.| 售价x | 33 | 35 | 37 | 39 | 41 | 43 | 45 | 47 |
| 销量y | 840 | 800 | 740 | 695 | 640 | 580 | 525 | 460 |
| $\hat y=-1200lnx+5000$ | $\hat y=-27x+1700$ | $\hat y=-\frac{1}{3}{x^2}+1200$ | |
| ${\sum_{i=1}^8{({{y_i}-{{\hat y}_i}})}^2}$ | 49428.74 | 11512.43 | 175.26 |
| ${\sum_{i=1}^8{({{y_i}-\overline y})}^2}$ | 124650 | ||
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2$\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | -$\frac{\sqrt{2}}{4}$ | D. | $\frac{\sqrt{2}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -3 | C. | 0 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\sqrt{5}$ | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com