
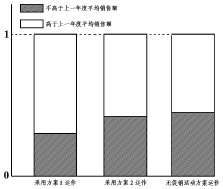
 某公司为评估两套促销活动方案(方案1运作费用为5元/件;方案2的运作费用为2元/件),在某地区部分营销网点进行试点(每个试点网点只采用一种促销活动方案),运作一年后,对比该地区上一年度的销售情况,制作相应的等高条形图如图所示.
某公司为评估两套促销活动方案(方案1运作费用为5元/件;方案2的运作费用为2元/件),在某地区部分营销网点进行试点(每个试点网点只采用一种促销活动方案),运作一年后,对比该地区上一年度的销售情况,制作相应的等高条形图如图所示.| 售价x | 33 | 35 | 37 | 39 | 41 | 43 | 45 | 47 |
| 销量y | 840 | 800 | 740 | 695 | 640 | 580 | 525 | 460 |
| $\hat y=-1200lnx+5000$ | $\hat y=-27x+1700$ | $\hat y=-\frac{1}{3}{x^2}+1200$ | |
| ${\sum_{i=1}^8{({{y_i}-{{\hat y}_i}})}^2}$ | 49428.74 | 11512.43 | 175.26 |
| ${\sum_{i=1}^8{({{y_i}-\overline y})}^2}$ | 124650 | ||
分析 (1)由等高条形图可知,年度平均销售额与方案1的运作相关性强于方案2.
(2)①求出相关指数,比较可得结论;
②由(1)可知,采用方案1的运作效果较方案2好,故年利润$z=({-\frac{1}{3}{x^2}+1200})({x-15})$,利用导数的方法,可得结论.
解答 解:(1)由等高条形图可知,年度平均销售额与方案1的运作相关性强于方案2.
(2)①由已知数据可知,回归模型$\hat y=-1200lnx+5000$对应的相关指数$R_1^2=0.6035$;
回归模型$\hat y=-27x+1700$对应的相关指数$R_2^2=0.9076$;
回归模型$\hat y=-\frac{1}{3}{x^2}+1200$对应的相关指数$R_3^2=0.9986$.
因为$R_3^2>R_2^2>R_1^2$,所以采用回归模型$\hat y=-\frac{1}{3}{x^2}+1200$进行拟合最为合适.
②由(1)可知,采用方案1的运作效果较方案2好,
故年利润$z=({-\frac{1}{3}{x^2}+1200})({x-15})$,z'=-(x+30)(x-40),
当x∈(0,40)时,$z=({-\frac{1}{3}{x^2}+1200})({x-15})$单调递增;
当x∈(40,+∞)时,$z=({-\frac{1}{3}{x^2}+1200})({x-15})$单调递减,
故当售价x=40时,利润达到最大.
点评 本题考查相关指数,考查等高条形图,考查导数知识的运用,属于中档题.


科目:高中数学 来源: 题型:选择题
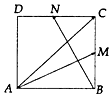 如图,在正方形ABCD中,M,N分别是BC,CD的中点,若$\overrightarrow{AC}=λ\overrightarrow{AM}+μ\overrightarrow{BN}$,则λ+μ的值为( )
如图,在正方形ABCD中,M,N分别是BC,CD的中点,若$\overrightarrow{AC}=λ\overrightarrow{AM}+μ\overrightarrow{BN}$,则λ+μ的值为( )| A. | $\frac{8}{5}$ | B. | $\frac{5}{8}$ | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{25}$ | B. | $\frac{16}{25}$ | C. | $\frac{49}{100}$ | D. | $\frac{49}{200}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,0] | B. | [0,2] | C. | [2,4] | D. | [-1,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 50π | B. | 100π | C. | 200π | D. | 300π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2\sqrt{5}}}{5}$ | B. | $\frac{7}{9}$ | C. | $\frac{4}{5}$ | D. | $\sqrt{13}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com