
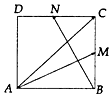
 如图,在正方形ABCD中,M,N分别是BC,CD的中点,若$\overrightarrow{AC}=λ\overrightarrow{AM}+μ\overrightarrow{BN}$,则λ+μ的值为( )
如图,在正方形ABCD中,M,N分别是BC,CD的中点,若$\overrightarrow{AC}=λ\overrightarrow{AM}+μ\overrightarrow{BN}$,则λ+μ的值为( )| A. | $\frac{8}{5}$ | B. | $\frac{5}{8}$ | C. | 1 | D. | -1 |
分析 根据向量的平行四边形法则和三角形法则和向量的数乘运算即可求出
解答 解:∵$\overrightarrow{AM}$=$\overrightarrow{AB}$+$\overrightarrow{BM}$=$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{BC}$=$\overrightarrow{DC}$+$\frac{1}{2}$$\overrightarrow{BC}$,
$\overrightarrow{BN}$=$\overrightarrow{BC}$+$\overrightarrow{CN}$=$\overrightarrow{BC}$-$\frac{1}{2}$$\overrightarrow{DC}$,
∴$\overrightarrow{BC}$=$\frac{2}{5}$$\overrightarrow{AM}$+$\frac{4}{5}$$\overrightarrow{BN}$,$\overrightarrow{DC}$=$\frac{4}{5}$$\overrightarrow{AM}$-$\frac{2}{5}$$\overrightarrow{BN}$
∴$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{BC}$=$\overrightarrow{DC}$+$\overrightarrow{BC}$=$\frac{2}{5}$$\overrightarrow{AM}$+$\frac{4}{5}$$\overrightarrow{BN}$+$\frac{4}{5}$$\overrightarrow{AM}$-$\frac{2}{5}$$\overrightarrow{BN}$=$\frac{6}{5}$$\overrightarrow{AM}$+$\frac{2}{5}$$\overrightarrow{BN}$,
∵$\overrightarrow{AC}=λ\overrightarrow{AM}+μ\overrightarrow{BN}$,
∴λ=$\frac{6}{5}$,μ=$\frac{2}{5}$,
∴λ+μ=$\frac{8}{5}$,
故选:A
点评 本题考查了向量的平行四边形法则和三角形法则和向量的数乘运算,属于基础题


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {(3,0),(0,2)} | C. | [一2,2] | D. | [一3,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2倍以上,但不超过3倍 | B. | 3倍以上,但不超过4倍 | ||
| C. | 4倍以上,但不超过5倍 | D. | 5倍以上,但不超过6倍 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
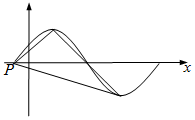 已知函数$f(x)=sin2x+sin(\frac{π}{3}-2x)$.
已知函数$f(x)=sin2x+sin(\frac{π}{3}-2x)$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{4}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
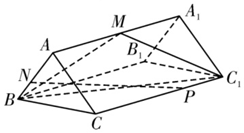 如图,已知三棱柱ABC-A1B1C1的底面ABC是等边三角形,且AA1⊥底面ABC,M为AA1的中点,N在线段AB上,且AN=2NB,点P在CC1上.
如图,已知三棱柱ABC-A1B1C1的底面ABC是等边三角形,且AA1⊥底面ABC,M为AA1的中点,N在线段AB上,且AN=2NB,点P在CC1上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
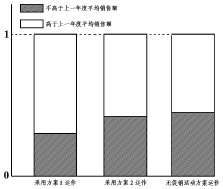 某公司为评估两套促销活动方案(方案1运作费用为5元/件;方案2的运作费用为2元/件),在某地区部分营销网点进行试点(每个试点网点只采用一种促销活动方案),运作一年后,对比该地区上一年度的销售情况,制作相应的等高条形图如图所示.
某公司为评估两套促销活动方案(方案1运作费用为5元/件;方案2的运作费用为2元/件),在某地区部分营销网点进行试点(每个试点网点只采用一种促销活动方案),运作一年后,对比该地区上一年度的销售情况,制作相应的等高条形图如图所示.| 售价x | 33 | 35 | 37 | 39 | 41 | 43 | 45 | 47 |
| 销量y | 840 | 800 | 740 | 695 | 640 | 580 | 525 | 460 |
| $\hat y=-1200lnx+5000$ | $\hat y=-27x+1700$ | $\hat y=-\frac{1}{3}{x^2}+1200$ | |
| ${\sum_{i=1}^8{({{y_i}-{{\hat y}_i}})}^2}$ | 49428.74 | 11512.43 | 175.26 |
| ${\sum_{i=1}^8{({{y_i}-\overline y})}^2}$ | 124650 | ||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com