
| A. | $\frac{{2\sqrt{5}}}{5}$ | B. | $\frac{7}{9}$ | C. | $\frac{4}{5}$ | D. | $\sqrt{13}$ |
分析 目标函数z=x2+y2的取值为原点O到可行域内任一点P距离的平方;
画出可行域,找出最优解是点O到直线x+2y=2的距离d,
从而求出目标函数z=x2+y2的最小值.
解答 解:目标函数z=x2+y2的取值即为原点O(0,0)到平面区域内任一点P距离的平方;
实数x,y满足$\left\{\begin{array}{l}{-x+y≤1}\\{x+2y≥2}\\{x-2≤0}\end{array}\right.$的平面区域是如图中A,B,C三点围成的三角形区域,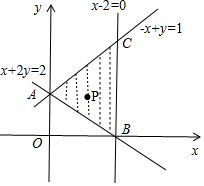
由图得:只有当取点O到直线x+2y=2的距离时,
O(0,0)到平面区域ABC内一点的距离最小;
点O到直线x+2y=2的距离为d=$\frac{|0+0-2|}{\sqrt{{1}^{2}{+2}^{2}}}$=$\frac{2\sqrt{5}}{5}$,
∴目标函数z=x2+y2的最小值是d2=${(\frac{2\sqrt{5}}{5})}^{2}$=$\frac{4}{5}$.
故选:C.
点评 本题主要考查了简单的线性规划问题,解题的关键在于分析出目标函数z=x2+y2的取值即为O(0,0)到平面区域内任一点距离的平方.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:解答题
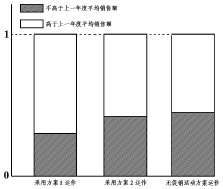 某公司为评估两套促销活动方案(方案1运作费用为5元/件;方案2的运作费用为2元/件),在某地区部分营销网点进行试点(每个试点网点只采用一种促销活动方案),运作一年后,对比该地区上一年度的销售情况,制作相应的等高条形图如图所示.
某公司为评估两套促销活动方案(方案1运作费用为5元/件;方案2的运作费用为2元/件),在某地区部分营销网点进行试点(每个试点网点只采用一种促销活动方案),运作一年后,对比该地区上一年度的销售情况,制作相应的等高条形图如图所示.| 售价x | 33 | 35 | 37 | 39 | 41 | 43 | 45 | 47 |
| 销量y | 840 | 800 | 740 | 695 | 640 | 580 | 525 | 460 |
| $\hat y=-1200lnx+5000$ | $\hat y=-27x+1700$ | $\hat y=-\frac{1}{3}{x^2}+1200$ | |
| ${\sum_{i=1}^8{({{y_i}-{{\hat y}_i}})}^2}$ | 49428.74 | 11512.43 | 175.26 |
| ${\sum_{i=1}^8{({{y_i}-\overline y})}^2}$ | 124650 | ||
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{π}{9}$,$\frac{5π}{18}$) | B. | [$\frac{π}{9}$,$\frac{π}{3}$) | C. | ($\frac{π}{12}$,$\frac{5π}{18}$) | D. | [$\frac{π}{18}$,$\frac{5π}{12}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\sqrt{5}$ | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}-1$ | B. | $\sqrt{5}+1$ | C. | $2\sqrt{5}+2$ | D. | $2\sqrt{5}-2$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com