
分析 根据题意,左边是n个数和的形式,右边是积的形式,一项为$\frac{n}{2}$,另一项成等差数列,规律为3n+1,即可得出结论.
解答 解:由题意,1+1=$\frac{1}{2}$×4
(2+1)+(2+2)=1×7
(3+1)+(3+2)+(3+3)=$\frac{3}{2}$×10
(4+1)+(4+2)+(4+3)+(4+4)=2×13
…
按照此规律,则(n+1)+(n+2)+(n+3)+…+(n+n)=$\frac{n}{2}×(3n+1)$,
故答案为$\frac{n}{2}×(3n+1)$.
点评 通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力.本题的关键是得出左边是n个数和的形式,右边是积的形式,一项为$\frac{n}{2}$,另一项成等差数列,规律为3n+1.


 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:填空题
| x | 1 | 2 | 3 | 4 | 5 |
| y | 13.2 | m | 14.2 | 15.4 | 16.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2\sqrt{5}}}{5}$ | B. | $\frac{7}{9}$ | C. | $\frac{4}{5}$ | D. | $\sqrt{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
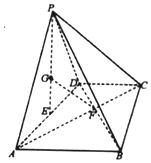 如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,底面ABCD为梯形,AB∥CD,AB=2DC=2$\sqrt{3}$,且△PAD与△ABD均为正三角形,E为AD的中点,G为△PAD的重心,AC∩BD=F
如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,底面ABCD为梯形,AB∥CD,AB=2DC=2$\sqrt{3}$,且△PAD与△ABD均为正三角形,E为AD的中点,G为△PAD的重心,AC∩BD=F查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4032 | B. | 2016 | C. | 4034 | D. | 2017 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com