
分析 根据△OAB是以O为直角顶点的等腰直角三角形,得到向量垂直和向量模长相等的条件,利用向量数量积的定义进行求解即可.
解答 解:若△OAB是以O为直角顶点的等腰直角三角形,
则$\overrightarrow{OA}$⊥$\overrightarrow{OB}$,即$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,
则($\overrightarrow{a}$-$\overrightarrow{b}$)•($\overrightarrow{a}$+$\overrightarrow{b}$)=0,
即|$\overrightarrow{a}$|2-|$\overrightarrow{b}$|2=0,
则|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=$\sqrt{2}$,
又|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|,
即|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$+$\overrightarrow{b}$|,
平方得|$\overrightarrow{a}$|2+|$\overrightarrow{b}$|2-2$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$|2+|$\overrightarrow{b}$|2+2$\overrightarrow{a}$•$\overrightarrow{b}$,
得$\overrightarrow{a}$•$\overrightarrow{b}$=0,
则|$\overrightarrow{OA}$|2=|$\overrightarrow{a}$|2+|$\overrightarrow{b}$|2-2$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$|2+|$\overrightarrow{b}$|2=2+2=4,
则|$\overrightarrow{OA}$|=2,
则△OAB的面积S=$\frac{1}{2}$|$\overrightarrow{OA}$|•|$\overrightarrow{OB}$|=$\frac{1}{2}×2×2$=2.
故答案为:2
点评 本题主要考查向量数量积的应用,根据等腰直角三角形的性质,结合向量垂直和向量相等的关系进行转化求解是解决本题的关键.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,3) | B. | [-1,3) | C. | (-1,3) | D. | (-3,-1] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
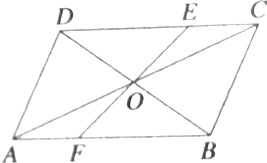 点O是平行四边形ABCD的中点,E,F分别在边CD,AB上,且$\frac{CE}{ED}$=$\frac{AF}{FB}$=$\frac{1}{2}$.求证:点E,O,F在同一直线上.
点O是平行四边形ABCD的中点,E,F分别在边CD,AB上,且$\frac{CE}{ED}$=$\frac{AF}{FB}$=$\frac{1}{2}$.求证:点E,O,F在同一直线上.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\sqrt{7}$,-1) | B. | (-$\sqrt{7}$,-1] | C. | (-$\sqrt{7}$,-2) | D. | (-$\sqrt{7}$,-2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com