
【题目】已知椭圆![]() 的中心在坐标原点
的中心在坐标原点![]() ,焦点在
,焦点在![]() 轴上,椭圆
轴上,椭圆![]() 的短轴端点和焦点所组成的四边形为正方形,且椭圆
的短轴端点和焦点所组成的四边形为正方形,且椭圆![]() 上任意一点到两个焦点的距离之和为
上任意一点到两个焦点的距离之和为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)若直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,函数
上是增函数,函数![]() 在
在![]() 上有三个零点.
上有三个零点.
(1)求![]() 的值;
的值;
(2)若1是其中一个零点,求![]() 的取值范围;
的取值范围;
(3)若![]() ,试问过点(2,5)可作多少条直线与曲线y=g(x)相切?请说明理由.
,试问过点(2,5)可作多少条直线与曲线y=g(x)相切?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|﹣ ![]() +a,x∈[1,6],a∈R.
+a,x∈[1,6],a∈R.
(1)若a=1,试判断并证明函数f(x)的单调性;
(2)当a∈(1,6)时,求函数f(x)的最大值的表达式M(a).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,抛物线C1:x2=4y,C2:x2=-2py(p>0).点M(x0,y0)在抛物线C2上,过M作C1的切线,切点为A,B(M为原点O时,A,B重合于O).当x0=1-![]() 时,切线MA的斜率为-
时,切线MA的斜率为-![]() .
.
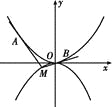
(1)求p的值;
(2)当M在C2上运动时,求线段AB中点N的轨迹方程(A,B重合于O时,中点为O).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足:a3=3,a5+a7=12,{an}的前n项和为Sn .
(1)求an及Sn;
(2)令bn= ![]() (n∈N*),求数列{bn}的前n项和Tn .
(n∈N*),求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个内角A,B,C,满足sinC= ![]() .
.
(1)判断△ABC的形状;
(2)设三边a,b,c成等差数列且S△ABC=6cm2 , 求△ABC三边的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系内,已知A(3,3)是⊙C上一点,折叠该圆两次使点A分别与圆上不相同的两点(异于点A)重合,两次的折痕方程分别为x﹣y+1=0和x+y﹣7=0,若⊙C上存在点P,使∠MPN=90°,其中M,N的坐标分别为(﹣m,0)(m,0),则m的最大值为( )
A.4
B.5
C.6
D.7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某气象站观测点记录的连续4天里, ![]() 指数
指数![]() 与当天的空气水平可见度
与当天的空气水平可见度![]() (单位
(单位![]() )的情况如下表1:
)的情况如下表1:
![]()
哈尔滨市某月![]() 指数频数分布如下表2:
指数频数分布如下表2:
![]()
(1)设![]() ,根据表1的数据,求出
,根据表1的数据,求出![]() 关于
关于![]() 的回归方程;
的回归方程;
(参考公式: ![]() ,其中
,其中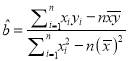 ,
, ![]() )
)
(2)小张开了一家洗车店,经统计,当![]() 不高于200时,洗车店平均每天亏损约2000元;当
不高于200时,洗车店平均每天亏损约2000元;当![]() 在
在![]() 时,洗车店平均每天收入约4000元;当
时,洗车店平均每天收入约4000元;当![]() 大于400时,洗车店平均每天收入约7000元;根据表2估计校长的洗车店该月份平均每天的收入.
大于400时,洗车店平均每天收入约7000元;根据表2估计校长的洗车店该月份平均每天的收入.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com