
| A. | -3 | B. | 3 | C. | 4 | D. | -2 |
分析 作出不等式组对应的平面区域,利用z的几何意义,利用数形结合即可得到结论.
解答 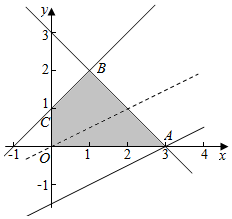 解:作出不等式组对应的平面区域如图:
解:作出不等式组对应的平面区域如图:
由z=x-2y,得y=$\frac{1}{2}x-\frac{z}{2}$
平移直线y=$\frac{1}{2}x-\frac{z}{2}$,由图象可知当直线y=$\frac{1}{2}x-\frac{z}{2}$经过点A(3,0)时,直线y=$\frac{1}{2}x-\frac{z}{2}$的截距最小,
此时z最大,此时zmax=3-2×0=3.
故选:B.
点评 本题主要考查线性规划的基本应用,利用目标函数的几何意义是解决问题的关键,利用数形结合是解决问题的基本方法.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
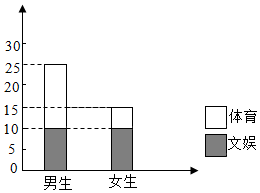 对某班学生是爱好体育还是爱好文娱进行调查,根据调查得到的数据,所绘制的二维条形图如图.
对某班学生是爱好体育还是爱好文娱进行调查,根据调查得到的数据,所绘制的二维条形图如图.| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
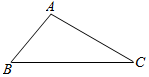 △ABC中,AB=1,AC=2.
△ABC中,AB=1,AC=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,3} | B. | {3,4} | C. | {$\sqrt{2}$,2,3} | D. | {2,3,4} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com