
 △ABC中,AB=1,AC=2.
△ABC中,AB=1,AC=2.分析 (1)由$\overrightarrow{AB}•\overrightarrow{AC}=\frac{1}{2}$便可得出$cos∠BAC=\frac{1}{4}$,可设D,E分别为AB,AC的中点,并连接OD,OE,设外接圆的半径为r,从而可得到$cos∠DAO=\frac{1}{2r},cos∠EAO=\frac{1}{r}$,进一步可以求出sin∠DAO,sin∠EAO,这样根据$cos(∠DAO+∠EAO)=\frac{1}{4}$便可建立关于r的方程,从而可解出r2,这样即可求出外接圆面积;
(2)在△ABC中,由余弦定理可以求得BC=2,从而∠BAC=∠B,从而有$cosB=\frac{1}{4}$,而cosC=-cos2B=$\frac{7}{8}$,进一步可求出sinB和sinC,从而由两角差的正弦公式即可求出sin(B-C)的值.
解答 解:(1)根据条件,$\overrightarrow{AB}•\overrightarrow{AC}=|\overrightarrow{AB}||\overrightarrow{AC}|cos∠BAC$=$2cos∠BAC=\frac{1}{2}$;
∴$cos∠BAC=\frac{1}{4}$,如图,设D,E分别为AB,AC的中点,连接OD,OE,则OD⊥AB,OE⊥AC,设外接圆的半径为r,则: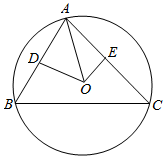 $cos∠DAO=\frac{1}{2r},cos∠EAO=\frac{1}{r}$;
$cos∠DAO=\frac{1}{2r},cos∠EAO=\frac{1}{r}$;
∴$sin∠DAO=\sqrt{1-\frac{1}{4{r}^{2}}}$,$sin∠EAO=\sqrt{1-\frac{1}{{r}^{2}}}$;
∴cos∠BAC=cos(∠DAO+∠EAO)=cos∠DAOcos∠EAO-sin∠DAOsin∠EAO=$\frac{1}{2{r}^{2}}-\sqrt{1-\frac{1}{4{r}^{2}}}•\sqrt{1-\frac{1}{{r}^{2}}}=\frac{1}{4}$;
解得${r}^{2}=\frac{16}{15}$;
∴△ABC外接圆面积为$\frac{16π}{15}$;
(2)如图, 在△ABC中,AB=1,AC=2,cos$∠BAC=\frac{1}{4}$;
在△ABC中,AB=1,AC=2,cos$∠BAC=\frac{1}{4}$;
∴由余弦定理得,BC2=1+4-1=4;
∴BC=2;
∴$cosB=\frac{1}{4}$,$cosC=cos(π-2B)=-2co{s}^{2}B+1=\frac{7}{8}$;
∴$sinB=\frac{\sqrt{15}}{4},sinC=\frac{\sqrt{15}}{8}$;
∴sin(B-C)=sinBcosC-cosBsinC=$\frac{\sqrt{15}}{4}×\frac{7}{8}-\frac{1}{4}×\frac{\sqrt{15}}{8}=\frac{3\sqrt{15}}{16}$.
点评 考查向量数量积的计算公式,三角形外接圆的定义,圆心和弦的中点的连线垂直于弦,余弦函数的定义,sin2x+cos2x=1,以及两角和差的正余弦公式,二倍角的余弦公式,余弦定理.


科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 3 | C. | 4 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{9}$ | B. | -$\frac{7}{9}$ | C. | $\frac{8}{9}$ | D. | -$\frac{8}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
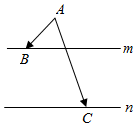 如图,在同一平面内,点A位于两平行直线m,n的同侧,且A到m,n的距离分别为1,3.点B、C分别在m、n上,$|{\overrightarrow{AB}+\overrightarrow{AC}}|=5$,则$\overrightarrow{AB}•\overrightarrow{AC}$的最大值是$\frac{21}{4}$.
如图,在同一平面内,点A位于两平行直线m,n的同侧,且A到m,n的距离分别为1,3.点B、C分别在m、n上,$|{\overrightarrow{AB}+\overrightarrow{AC}}|=5$,则$\overrightarrow{AB}•\overrightarrow{AC}$的最大值是$\frac{21}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}+ln2$ | B. | $\frac{1}{2}-ln2$ | C. | -1+ln2 | D. | 1+ln2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
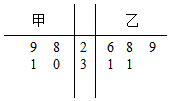 为比较甲、乙两地某月11时的气温情况,随机选取该月中的5天中11时的气温数据(单位:℃)制成如图所示的茎叶图,考虑以下结论:
为比较甲、乙两地某月11时的气温情况,随机选取该月中的5天中11时的气温数据(单位:℃)制成如图所示的茎叶图,考虑以下结论:| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
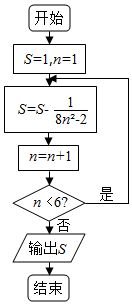
| A. | $\frac{7}{9}$ | B. | $\frac{17}{22}$ | C. | $\frac{10}{13}$ | D. | $\frac{23}{30}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com