
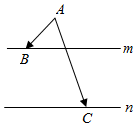
 如图,在同一平面内,点A位于两平行直线m,n的同侧,且A到m,n的距离分别为1,3.点B、C分别在m、n上,$|{\overrightarrow{AB}+\overrightarrow{AC}}|=5$,则$\overrightarrow{AB}•\overrightarrow{AC}$的最大值是$\frac{21}{4}$.
如图,在同一平面内,点A位于两平行直线m,n的同侧,且A到m,n的距离分别为1,3.点B、C分别在m、n上,$|{\overrightarrow{AB}+\overrightarrow{AC}}|=5$,则$\overrightarrow{AB}•\overrightarrow{AC}$的最大值是$\frac{21}{4}$. 分析 建立如图所示的坐标系,得到点A、B、C的坐标,由 $|{\overrightarrow{AB}+\overrightarrow{AC}}|=5$,求得a+b=±3,分类讨论,利用二次函数的性质求得$\overrightarrow{AB}•\overrightarrow{AC}$ 的最大值.
解答 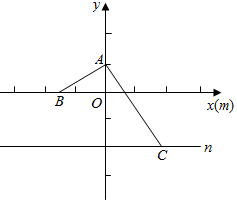 解:由点A位于两平行直线m,n的同侧,且A到m,n的
解:由点A位于两平行直线m,n的同侧,且A到m,n的
距离分别为1,3,
可得平行线m、n间的距离为2,
以直线m为x轴,以过点A且与直线m垂直的直线为y轴
建立坐标系,如图所示:
则由题意可得点A(0,1),直线n的方程为y=-2,
设点B(a,0)、点C(b,-2),
∴$\overrightarrow{AB}$=(a,-1)、$\overrightarrow{AC}$=(b,-3),
∴$\overrightarrow{AB}$+$\overrightarrow{AC}$=(a+b,-4).
∵$|{\overrightarrow{AB}+\overrightarrow{AC}}|=5$,∴(a+b)2+16=25,∴a+b=3,或a+b=-3.
当a+b=3时,$\overrightarrow{AB}•\overrightarrow{AC}$=ab+3=a(3-a)+3=-a2+3a+3,它的最大值为$\frac{-12-9}{-4}$=$\frac{21}{4}$.
当a+b=-3时,$\overrightarrow{AB}•\overrightarrow{AC}$=ab+3=a(-3-a)+3=-a2-3a+3,它的最大值为$\frac{-12-9}{-4}$=$\frac{21}{4}$.
综上可得,$\overrightarrow{AB}•\overrightarrow{AC}$ 的最大值为$\frac{21}{4}$,
故答案为:$\frac{21}{4}$.
点评 本题主要考查两个向量的数量积公式,两个向量坐标形式的运算,二次函数的性质,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
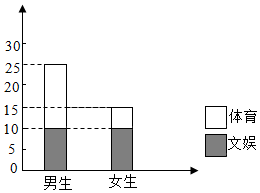 对某班学生是爱好体育还是爱好文娱进行调查,根据调查得到的数据,所绘制的二维条形图如图.
对某班学生是爱好体育还是爱好文娱进行调查,根据调查得到的数据,所绘制的二维条形图如图.| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 右平移$\frac{5π}{12}$个单位 | B. | 右平移$\frac{π}{12}$个单位 | ||
| C. | 左平移$\frac{π}{6}$个单位 | D. | 左平移$\frac{π}{12}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
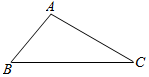 △ABC中,AB=1,AC=2.
△ABC中,AB=1,AC=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{22}{3}$ | B. | $\frac{26}{3}$ | C. | $\frac{34}{3}$ | D. | $-\frac{2}{27}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com