
分析 (1)由题意可得(x-lnx)a≤x2-2x,记F(x)=x-lnx,求出导数,求得最小值1,运用参数分离可得a≤$\frac{{x}^{2}-2x}{x-lnx}$,求出导数,求得单调区间、极值和最值,即可得到a的范围;
(2)求出f(x)的导数,假设f(x)是“中值平衡函数”,则存在A(x1,f(x1)),B(x2,f(x2))(0<x1<x2),求出切线的斜率,运用两点的斜率公式,可得$\frac{2a}{{{x_1}+{x_2}}}=\frac{{a(ln{x_2}-ln{x_1})}}{{{x_2}-{x_1}}}$,讨论a是否为0,构造函数求出导数,判断单调性,结合新定义,即可得到所求“中值平衡切线”的条数.
解答 解:(1)由f(x)≥g(x),得$(x-lnx)a≤x_{\;}^2-2x$,
记F(x)=x-lnx(x>0),${F^'}(x)=\frac{x-1}{x}(x>0)$,
当0<x<1时,F′(x)<0,F(x)递减,
当x>1时,F′(x)>0,F(x)递增;
所以F(x)≥F(1)=1>0,
∴a≤$\frac{{x}^{2}-2x}{x-lnx}$,记$G(x)=\frac{{{x^2}-2x}}{x-lnx},x∈[{\frac{1}{e},e}]$,
∴${G^'}(x)=\frac{(x-1)(x-2lnx+2)}{{{{(x-lnx)}^2}}}$,∵$x∈[{\frac{1}{e},e}]$,
∴x-2lnx+2=2(1-lnx)+x≥x>0,
∴$x∈[{\frac{1}{e},1})$时,G′(x)<0,G(x)递减;
x∈(1,e]时,G′(x)>0,G(x)递增;
∴G(x)min=G(1)=-1,∴a≤G(x)min=-1,
故实数a的取值范围为(-∞,-1];
(2)函数f(x)的定义域为(0,+∞),
${f^'}(x)=\frac{a}{x}+2x-4=\frac{{2{x^2}-4x+a}}{x}$,
若函数f(x)是“中值平衡函数”,
则存在A(x1,f(x1)),B(x2,f(x2))(0<x1<x2)
使得${f^'}({x_0})=\frac{{f({x_2})-f({x_1})}}{{{x_2}-{x_1}}}$,
即$\frac{2a}{{{x_1}+{x_2}}}+{x_1}+{x_2}-4=\frac{{a(ln{x_2}-ln{x_1})+x_2^2-x_1^2-4({x_2}-{x_1})}}{{{x_2}-{x_1}}}$,
∴$\frac{2a}{{{x_1}+{x_2}}}=\frac{{a(ln{x_2}-ln{x_1})}}{{{x_2}-{x_1}}}$(※)
①当a=0时,(※)对任意的0<x1<x2都成立,
所以函数f(x)是“中值平衡函数”,且函数f(x)的“中值平衡切线”有无数条;
②当a≠0时,有$\frac{2({x}_{2}-{x}_{1})}{{x}_{2}+{x}_{1}}$=ln$\frac{{x}_{2}}{{x}_{1}}$,
设t=$\frac{{x}_{2}}{{x}_{1}}$>1,则方程lnt=$\frac{2(t-1)}{t+1}$在区间(1,+∞)上有解,
记函数$h(t)=lnt-\frac{2(t-1)}{t+1},t>1$,
则${h^'}(t)=\frac{1}{t}-\frac{4}{{{{(t+1)}^2}}}=\frac{{{{(t-1)}^2}}}{{t{{(t+1)}^2}}}>0$,
所以函数h(t)在区间(1,+∞)递增,
∵h(1)=0,所以当t>1时,h(t)>h(1)=0,
即方程$lnt=\frac{2(t-1)}{t+1}$在区间(1,+∞)上无解,即函数f(x)不是“中值平衡函数”;
综上所述,当a=0时,函数f(x)是“中值平衡函数”,
且函数f(x)的“中值平衡切线”有无数条;
当a≠0时,f(x)不是“中值平衡函数”.
点评 本题考查导数的运用:求切线的斜率和单调区间、极值和最值,考查不等式恒成立问题的解法,注意运用分离参数,考查新定义的理解和运用,注意运用分类讨论的思想方法,考查构造函数的方法,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 3 | C. | 4 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{9}$ | B. | -$\frac{7}{9}$ | C. | $\frac{8}{9}$ | D. | -$\frac{8}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
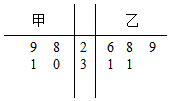 为比较甲、乙两地某月11时的气温情况,随机选取该月中的5天中11时的气温数据(单位:℃)制成如图所示的茎叶图,考虑以下结论:
为比较甲、乙两地某月11时的气温情况,随机选取该月中的5天中11时的气温数据(单位:℃)制成如图所示的茎叶图,考虑以下结论:| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com