
分析 利用对数的性质、运算法则、换底公式求解.
解答 解:(1)(0.008)${\;}^{\frac{1}{3}}}$+($\sqrt{2}$-π)0-(${\frac{125}{64}}$)${\;}^{-\frac{1}{3}}}$
=0.2+1-$\frac{4}{5}$
=$\frac{2}{5}$.
(2)$\frac{{({{log}_3}2+{{log}_9}2)•({{log}_4}3+{{log}_8}3)}}{{lg600-\frac{1}{2}lg0.036-\frac{1}{2}lg0.1}}$
=$\frac{(lo{g}_{9}4+lo{g}_{9}2)•(lo{g}_{64}27+lo{g}_{64}9)}{lg600-lg\sqrt{0.036}-lg\sqrt{0.1}}$
=$\frac{lo{g}_{9}8•lo{g}_{64}243}{lg\frac{600}{\sqrt{0.0036}}}$
=$\frac{\frac{lg8}{lg9}×\frac{lg243}{lg64}}{lg1000}$
=$\frac{5}{4}$.
点评 本题考查对数的化简求值,注意对数的性质、运算法则、换底公式的合理运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
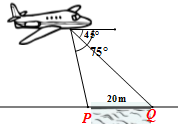 如图,从一架飞机上观察前下方河流两岸P、Q两点的俯角分别为75°、45°,已知河的宽度|PQ|=20m,则此时飞机的飞行高度为$10(\sqrt{3}+1)$m.
如图,从一架飞机上观察前下方河流两岸P、Q两点的俯角分别为75°、45°,已知河的宽度|PQ|=20m,则此时飞机的飞行高度为$10(\sqrt{3}+1)$m.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | -1 | D. | -2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com