
| A. | (1,+∞) | B. | (1,$\sqrt{2}$) | C. | ($\sqrt{2}$,+∞) | D. | (0,1) |
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∨(¬q) | C. | (¬p)∧q | D. | (¬p)∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
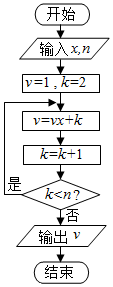 如图所示的程序框图的算法思路源于我国古代数字著作《数书九章》,称为“秦九韶算法”.执行该程序框图,若输入x=2,n=5,则输出的v=( )
如图所示的程序框图的算法思路源于我国古代数字著作《数书九章》,称为“秦九韶算法”.执行该程序框图,若输入x=2,n=5,则输出的v=( )| A. | 26 | B. | 48 | C. | 57 | D. | 64 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
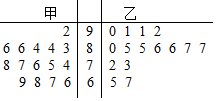 某农场用甲、乙两种不同的方式培育了一批甘蔗苗,培育一段时间后,同时随机抽取两种方式培育的甘蔗苗各15株,测量其高度,得到如图的茎叶图(单位:cm)
某农场用甲、乙两种不同的方式培育了一批甘蔗苗,培育一段时间后,同时随机抽取两种方式培育的甘蔗苗各15株,测量其高度,得到如图的茎叶图(单位:cm)| 甲方式 | 乙方式 | 合计 | |
| 优秀 | |||
| 不优秀 | |||
| 合计 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{7}$ | B. | $\frac{5}{3}$ | C. | $\frac{11}{7}$ | D. | $\frac{8}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-2<x<1} | B. | {x|-2<x<2} | C. | {x|2≤x<3} | D. | {x|x<2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com