考点:异面直线及其所成的角,棱柱、棱锥、棱台的体积
专题:计算题,空间位置关系与距离
分析:(I)过A1作A1H⊥平面ABC,垂足为H,证明H在∠CAB平分线上,根据AB=AC,可得BC⊥AA1,判断各侧面的形状,根据∠A1AB=∠A1AC=45°计算棱柱的高,利用面积公式与棱柱的体积公式计算;
(II)利用向量的数量积公式计算异面直线AA1与EF所成角的余弦值.
解答:
解:(Ⅰ)过A
1作A
1H⊥平面ABC,垂足为H,过H作HD⊥AB于D,连A
1D,则A
1D⊥AB,
作HF⊥AC于F,连A
1F,则A
1F⊥AC,
又∠A
1AB=∠A
1AC=45°,∴Rt△A
1AD≌Rt△A
1AF,AD=AF,
∴Rt△ADH≌Rt△AFH,从而H在∠CAB平分线上,
∵△ABC为正三角形,∴BC⊥AH,∴BC⊥AA
1,
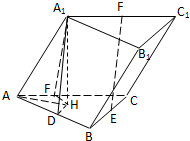
在Rt△A
1AD中,计算得A
1D=AD=1,在Rt△ADH中,计算得
DH=,在Rt△A
1DH中,计算得
A1H=,
∴棱柱的表面积
S=2S△ABC+2SABB1A1+SBCC1B1=+2+,
棱柱的体积
V=S△ABC.A1H=•=;
(Ⅱ)∵
=+=-(++AA1+=-,
∴
2=2+2-•=2+-×1×=,
解得
||=,
又
•=(-)•=2-×1××=,
∴cosθ=
=,
即异面直线AA
1与EF所成角的余弦值
.
点评:本题考查了棱锥的面积与体积计算,考查了异面直线所成角的求法及向量的应用,考查了学生的空间想象能力与计算能力,综合性强,运算要细心.

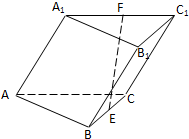 如图,斜三棱柱ABC-A1B1C1的侧棱长为
如图,斜三棱柱ABC-A1B1C1的侧棱长为


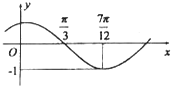 函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<
函数f(x)=Asin(ωx+φ)(其中A>0,|φ|< 如图,在棱长为a的正方体ABCD-A1B1C1D1中,M、N、P分别是棱DD1、CD、AD的中点.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,M、N、P分别是棱DD1、CD、AD的中点.