
| A. | $\frac{n(2n-1)}{2}$ | B. | 2(2n2-n) | C. | $\frac{n^2}{2}$ | D. | 2n2-n |
分析 由给出的数列是等比数列,结合a3•a2n-3=32n(n≥2),利用等比中项的概念求出an,利用对数式的运算性质化简要求值的式子,把an代入后在运用等差数列的求和化简即可得到答案.
解答 解:在等比数列{an}中,由a3•a2n-3=32n(n≥2),
得:a2n=a3•a2n-3=32n(n≥2),.
因为an>0,所以an=3n.
∴${log_{\sqrt{3}}}{a_{2n-1}}$=2log3a2n-1=2log332n-1=2(2n-1)
则${log_{\sqrt{3}}}{a_1}$+${log_{\sqrt{3}}}{a_2}$+…+${log_{\sqrt{3}}}{a_{2n-1}}$=2(1+2+3+…+2n-1)=2•$\frac{(2n-1)(2n-1+1)}{2}$=2(n2-n),
故选:B
点评 本题考查了等比数列的通项公式,考查了对数式的运算性质,利用等比中项的概念求出an是解答该题的关键,此题是中档题.


科目:高中数学 来源: 题型:解答题
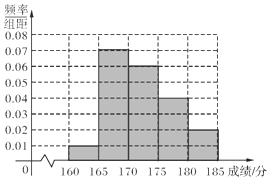 某校在2016年的自主招生考试成绩中随机抽取100名学生的笔试成绩,被抽取学生的成绩均不低于160分,且低于185分,如图是按成绩分组得到的频率分布直方图.
某校在2016年的自主招生考试成绩中随机抽取100名学生的笔试成绩,被抽取学生的成绩均不低于160分,且低于185分,如图是按成绩分组得到的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(1,\sqrt{2})$ | B. | $(1,\sqrt{3})$ | C. | $(\sqrt{2},2)$ | D. | $(\sqrt{3},2)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1)(2) | B. | (2)(3) | C. | (1)(3) | D. | (3)(4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com