
分析 根据正弦定理化简已知式子,由二倍角的余弦公式变形、和差化积公式和诱导公式化简后,由内角的范围和正弦函数的性质求出A与B关系,由锐角三角形的条件求出B的范围,利用商得关系、两角差的正弦公式化简所求的式子,由正弦函数的性质求出所求式子的取值范围.
解答 解:∵b2-a2=ac,
∴由正弦定理得,sin2B-sin2A=sinAsinC,
$\frac{1-cos2B}{2}-\frac{1-cos2A}{2}$=sinAsinC,
$\frac{cos2A-cos2B}{2}=sinAsinC$,
由和差化积公式得cos2A-cos2B=-2sin(A+B)sin(A-B),代入上式得,
-sin(A+B)sin(A-B)=sinAsinC,
∵sin(A+B)=sinC≠0,
∴-sin(A-B)=sinA,即sin(B-A)=sinA,
在△ABC中,B-A=A,得B=2A,则C=π-3A,
∵△ABC为锐角三角形,
∴$\left\{\begin{array}{l}{0<2A<\frac{π}{2}}\\{0<π-3A<\frac{π}{2}}\end{array}\right.$,
解得$\frac{π}{6}$$<A<\frac{π}{4}$,则$\frac{π}{3}<B<\frac{π}{2}$,
∴$\frac{1}{tanA}-\frac{1}{tanB}$=$\frac{cosA}{sinA}-\frac{cosB}{sinB}$=$\frac{cosAsinB-sinAcosB}{sinAsinB}$
=$\frac{sin(B-A)}{sinAsinB}=\frac{1}{sinB}$,
由$\frac{π}{3}<B<\frac{π}{2}$得,sinB∈($\frac{\sqrt{3}}{2}$,1),则$\frac{1}{sinB}$∈(1,$\frac{2\sqrt{3}}{3}$),
∴$\frac{1}{tanA}-\frac{1}{tanB}$取值范围是(1,$\frac{2\sqrt{3}}{3}$).
故答案为:$(1,\frac{{2\sqrt{3}}}{3})$.
点评 本题是综合题,考查了正弦定理,三角恒等变换中公式,以及正弦函数的性质,涉及知识点多、公式多,综合性强,考查化简、变形能力,属于中档题.


 小学教材全测系列答案
小学教材全测系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}+\frac{{\sqrt{3}}}{18}π$ | B. | $\frac{1}{2}+\frac{{\sqrt{3}}}{18}π$ | C. | $\frac{3}{4}-\frac{{\sqrt{3}}}{18}π$ | D. | $\frac{1}{2}-\frac{{\sqrt{3}}}{18}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 体积(升/件) | 重量(公斤/件) | 利润(元/件) | |
| 甲 | 20 | 10 | 8 |
| 乙 | 10 | 20 | 10 |
| A. | 65元 | B. | 62元 | C. | 60元 | D. | 56元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
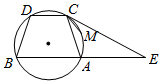 如图,已知圆上的$\widehat{AC}$=$\widehat{BD}$,过C点的圆的切线与BA的延长线交于E点,设M是$\widehat{AC}$的中点,
如图,已知圆上的$\widehat{AC}$=$\widehat{BD}$,过C点的圆的切线与BA的延长线交于E点,设M是$\widehat{AC}$的中点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com