
| A. | $\frac{1}{4}+\frac{{\sqrt{3}}}{18}π$ | B. | $\frac{1}{2}+\frac{{\sqrt{3}}}{18}π$ | C. | $\frac{3}{4}-\frac{{\sqrt{3}}}{18}π$ | D. | $\frac{1}{2}-\frac{{\sqrt{3}}}{18}π$ |
分析 以BC为直径作圆,根据圆周角定理得到P的位置,计算器面积,利用几何概型的公式解之.
解答 解:如图所示: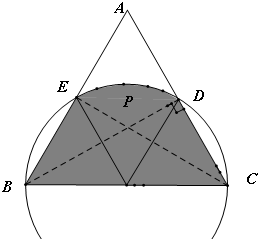 以BC为直径作圆,与AB,AC分别相交于E,D,则P在图中阴影部分,即使得△BCP为钝角三角形,
以BC为直径作圆,与AB,AC分别相交于E,D,则P在图中阴影部分,即使得△BCP为钝角三角形,
设等边三角形吧边长为2,则阴影部分的面积为2×$\frac{\sqrt{3}}{4}×{1}^{2}$+$\frac{1}{6}π×{1}^{2}$=$\frac{\sqrt{3}}{2}+\frac{π}{6}$,等
边三角形的面积为$\frac{\sqrt{3}}{4}×{2}^{2}=\sqrt{3}$,
由几何概型的概率公式得到△BCP为钝角三角形的概率为:$\frac{\frac{\sqrt{3}}{2}+\frac{π}{6}}{\sqrt{3}}=\frac{1}{2}+\frac{\sqrt{3}}{18}π$;
故选:B.
点评 本题主要考查了几何概率的求解,体现了转化、数形结合的数学思想,关键是明确满足条件的P的区域面积.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,2] | B. | [-2,-1] | C. | (1,2] | D. | [-2,-1)∪(1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
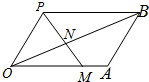 如图所示,四边形OABP是平行四边形,过点P的直线与射线OA、OB分别相交于点M、N,若$\overrightarrow{OM}$=x$\overrightarrow{OA}$,$\overrightarrow{ON}$=y$\overrightarrow{OB}$.
如图所示,四边形OABP是平行四边形,过点P的直线与射线OA、OB分别相交于点M、N,若$\overrightarrow{OM}$=x$\overrightarrow{OA}$,$\overrightarrow{ON}$=y$\overrightarrow{OB}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 感染 | 未感染 | 总计 | |
| 服用 | 10 | 40 | 50 |
| 未服用 | 20 | 30 | 50 |
| 总计 | 30 | 70 | 100 |
| P(K2>k) | 0.10 | 0.05 | 0.025 |
| k | 2.706 | 3.841 | 5.024 |
| A. | 在犯错误的概率不超5%过的前提下,认为“小动物是否被感染与有没有服用疫苗有关” | |
| B. | 在犯错误的概率不超5%过的前提下,认为“小动物是否被感染与有没有服用疫苗无关” | |
| C. | 有97.5%的把握认为“小动物是否被感染与有没有服用疫苗有关” | |
| D. | 有97.5%的把握认为“小动物是否被感染与有没有服用疫苗无关” |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com