
分析 (1)化简函数f(x)为正弦型函数,即可求出它的最小正周期;
(2)根据正弦函数的图象与性质,即可求出f(x)图象的对称轴方程与对称中心的坐标.
解答 解:(1)函数f(x)=sinxcosx-$\sqrt{3}$cos2x+$\frac{\sqrt{3}}{2}$
=$\frac{1}{2}$sin2x-$\sqrt{3}$•$\frac{1+cos2x}{2}$+$\frac{\sqrt{3}}{2}$
=$\frac{1}{2}$sin2x-$\frac{\sqrt{3}}{2}$cos2x
=sin(2x-$\frac{π}{3}$),
∴f(x)的最小正周期为T=$\frac{2π}{2}$=π;
(2)∵函数f(x)=sin(2x-$\frac{π}{3}$),
令2x-$\frac{π}{3}$=$\frac{π}{2}$+kπ,k∈Z,
解得x=$\frac{5π}{12}$+$\frac{kπ}{2}$,k∈Z,
∴f(x)图象的对称轴方程为:x=$\frac{5π}{12}$+$\frac{kπ}{2}$,k∈Z;
再令2x-$\frac{π}{3}$=kπ,k∈Z,
解得x=$\frac{π}{6}$+$\frac{kπ}{2}$,k∈Z,
∴f(x)图象的对称中心的坐标为($\frac{π}{6}$+$\frac{kπ}{2}$,0),k∈Z.
点评 本题考查了三角函数的图象与性质的应用问题,也考查了三角恒等变换的应用问题,是基础题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{5}$ | B. | $\frac{6}{5}$ | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 感染 | 未感染 | 总计 | |
| 服用 | 10 | 40 | 50 |
| 未服用 | 20 | 30 | 50 |
| 总计 | 30 | 70 | 100 |
| P(K2>k) | 0.10 | 0.05 | 0.025 |
| k | 2.706 | 3.841 | 5.024 |
| A. | 在犯错误的概率不超5%过的前提下,认为“小动物是否被感染与有没有服用疫苗有关” | |
| B. | 在犯错误的概率不超5%过的前提下,认为“小动物是否被感染与有没有服用疫苗无关” | |
| C. | 有97.5%的把握认为“小动物是否被感染与有没有服用疫苗有关” | |
| D. | 有97.5%的把握认为“小动物是否被感染与有没有服用疫苗无关” |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
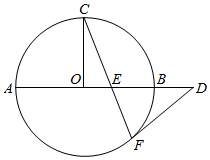 如图,AB是⊙O的直径,C、F是⊙O上的两点,OC⊥AB,过点F作⊙O的切线FD交AB的延长线于点D,连接CF交AB于点E.
如图,AB是⊙O的直径,C、F是⊙O上的两点,OC⊥AB,过点F作⊙O的切线FD交AB的延长线于点D,连接CF交AB于点E.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com