
分析 构造函数g(x)=ax3-4ax2-$\frac{1}{2}x$+1,则x1,x2为g(x)的两个零点,利用零点的存在性定理可知g(x)在(0,$\frac{1}{2}$),(4,$\frac{9}{2}$)上分别存在一个零点,利用不等式的性质即可得出结论.
解答 证明:f(x)=x(ax3-4ax2-$\frac{1}{2}x$+1),设g(x)=ax3-4ax2-$\frac{1}{2}x$+1,
则g(x)在(0,+∞)上有两个零点x1,x2,
不妨设x1<x2,∵g(0)=1>0,g($\frac{1}{2}$)=$\frac{1}{8}$(6-7a)<0,g(4)=-1<0,
g($\frac{9}{2}$)=$\frac{1}{8}$(657a-10)>0.
∴0<x1<$\frac{1}{2}$,4<x2<$\frac{9}{2}$,
∴4<x1+x2<5,
∵a>1,∴a+4>5,
∴4<x1+x2<a+4.
点评 本题考查了函数零点的存在性定理,不等式的性质,属于中档题.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:解答题
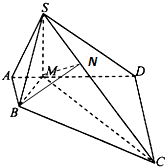 如图,在四棱锥S-ABCD中,AB⊥AD,AB∥CD,CD=3AB,平面SAD⊥平面ABCD,M是线段AD上一点,AM=AB,DM=DC,SM⊥AD.
如图,在四棱锥S-ABCD中,AB⊥AD,AB∥CD,CD=3AB,平面SAD⊥平面ABCD,M是线段AD上一点,AM=AB,DM=DC,SM⊥AD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
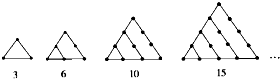 把3、6、10、15、21、…这些数叫做三角形数,这是因为这些数目的点子可以排成一个正三角形(如图),试求第六个三角形数是( )
把3、6、10、15、21、…这些数叫做三角形数,这是因为这些数目的点子可以排成一个正三角形(如图),试求第六个三角形数是( )| A. | 27 | B. | 28 | C. | 29 | D. | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-4,0) | B. | [0,4] | C. | (-6,0) | D. | [0,6] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 物理 成绩好 | 物理 成绩不好 | 合计 | |
| 数学 成绩好 | 62 | 23 | 85 |
| 数学 成绩不好 | 28 | 22 | 50 |
| 合计 | 90 | 45 | 135 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com