练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    从1,3,5,7,9五个数字中选2个，0,2,4,6,8五个数字中选3个，能组成多少个无重复数字的五位数？

    10 560(个)

    解析解：从5个奇数中选出2个，再从2、4、6、8四个偶数中选出3个，排成五位数，有C52·C43·A55＝4 800(个)．从5个奇数中选出2个，再从2,4,6,8四个偶数中再选出2个，将选出的4个数再选一个做万位数．余下的3个数加上0排在后4个数位上，有C52·C42·C41·A44＝10×6×4×24＝5 760(个)．由分类加法计数原理可知这样的五位数共有C52·C43·C52＋A55·C42·C41·A44＝10 560(个)．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    若的展开式中前三项系数成等差数列，
    求：（1）展开式中含的一次幂的项；
    （2）展开式中所有的有理项
    （3）展开式中系数最大的项

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知在的展开式中，第5项的系数与第3项的系数之比是．
    （1）求展开式中的所有有理项；
    （2）求展开式中系数绝对值最大的项；
    （3）求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知的展开式中前三项的系数成等差数列．设＝a0＋a1x＋a2x2＋…＋anxn.求：
    (1)a5的值；
    (2)a0－a1＋a2－a3＋…＋(－1)nan的值；
    (3)ai(i＝0，1，2，…，n)的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    设，且，其中当为偶数时，；当为奇数时，．
    （1）证明：当，时，；
    （2）记，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4位参加辩论比赛的同学，比赛规则是：每位同学必须从甲、乙两道题中任选一题做答，选甲题答对得100分，答错得－100分；选乙题答对得90分，答错得－90分．若4位同学的总分为0分，则这4位同学有多少种不同得分情况？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某运输公司有7个车队．每个车队的车都多于4辆且型号相同，要从这7个车队中抽出10辆车组成一运输车队，每个车队至少抽1辆车，则不同抽法有多少种？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

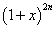    已知的展开式中偶数项二项式系数和比展开式中奇数项二项式系数和小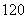，求：
    （I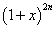）展开式中二项式系数最大的项；
    （II）设展开式中的常数项为p，展开式中所有项系数的和为q，求p+q.

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    二项式展开式中的常数项是第______项。

    查看答案和解析>>

    同步练习册答案