
【题目】设![]() .
.
(1)求![]() 的单调区间;
的单调区间;
(2)求![]() 在[-5,
在[-5, ![]() ]的最大值与最小值.
]的最大值与最小值.
【答案】(1)单调增区间为(-2, ![]() ),单调减区间为(-∞,-2)和(
),单调减区间为(-∞,-2)和(![]() ,+∞);(2)f (x)取最小值是0,f (x)取最大值是63.
,+∞);(2)f (x)取最小值是0,f (x)取最大值是63.
【解析】试题分析:
(1)求导可得f ′(x)= -(x+2)(3x-2),利用导函数研究函数的单调性可得单调增区间为(-2, ![]() ),单调减区间为(-∞,-2)和(
),单调减区间为(-∞,-2)和(![]() ,+∞);
,+∞);
(2)由题意结合(1)的结论考查极值和端点处的函数值可得x= -2时,f (x)取最小值0,x= -5时,f (x)取最大值63.
试题解析:
(1)f ′(x)= -(x+2)(3x-2),
令f ′(x)>0得 -2<x<![]() ,令f ′(x)<0得x<-2或x>
,令f ′(x)<0得x<-2或x>![]() ,
,
∴单调增区间为(-2, ![]() ),单调减区间为(-∞,-2)和(
),单调减区间为(-∞,-2)和(![]() ,+∞);
,+∞);
(2)由单调性可知,当x= -2时,f (x)有极小值f (-2 )=0,当x=![]() 时,f (x)有极大值f (
时,f (x)有极大值f (![]() )=
)=![]() ;
;
又f (-5)=63,f (![]() )=
)=![]() ,∴x= -2时,f (x)取最小值0,x= -5时,f (x)取最大值63.
,∴x= -2时,f (x)取最小值0,x= -5时,f (x)取最大值63.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱锥A﹣BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E、F(E与A、D不重合)分别在棱AD,BD上,且EF⊥AD. 求证:(Ⅰ)EF∥平面ABC;
(Ⅱ)AD⊥AC.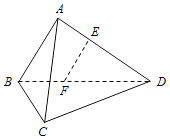
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是样本容量为200的频率分布直方图.根据样本的频率分布直方图估计,样本数落在[6,10]内的频数为 ,数据落在(2,10)内的概率约为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() 的前
的前![]() 项和为
项和为![]() ,若数列
,若数列![]() 的各项按如下规律排列:
的各项按如下规律排列:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,
,![]() , …,
, …,![]() ,…有如下运算和结论:①
,…有如下运算和结论:①![]() ;②数列
;②数列![]() ,
,![]() ,
,![]() ,
,![]() ,…是等比数列;③数列
,…是等比数列;③数列![]() ,
,![]() ,
,![]() ,
,![]() ,…的前
,…的前![]() 项和为
项和为![]() ;④若存在正整数
;④若存在正整数![]() ,使
,使![]() ,
,![]() ,则
,则![]() .其中正确的结论是_____.(将你认为正确的结论序号都填上)
.其中正确的结论是_____.(将你认为正确的结论序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A、B、C所对的边分别为a、b、c,若![]() =
=![]() .
.
(1)求角A;
(2)若f(x)=sinx+![]() cos(x+A),求函数f(x)的单调递增区间.
cos(x+A),求函数f(x)的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)设直线![]() 的方程为
的方程为![]() .若直线
.若直线![]() 在两坐标轴上的截距相等,求直线
在两坐标轴上的截距相等,求直线![]() 的方程;
的方程;
(2)过直线![]() :
:![]() 上的点
上的点![]() 作直线
作直线![]() ,若直线
,若直线![]() ,
,![]() 与
与![]() 轴围成的三角形的面积为2,则直线
轴围成的三角形的面积为2,则直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了弘扬民族文化,某中学举行了“我爱国学,传诵经典”考试,并从中随机抽取了60名学生的成绩(满分100分)作为样本,其中成绩不低于80分的学生被评为优秀生,得到成绩分布的频率分布直方图如图所示.

(1)若该所中学共有2000名学生,试利用样本估计全校这次考试中优秀生人数;
(2)(i)试估计这次参加考试的学生的平均成绩(同一组数据用该组区间的中点值作代表);
(ii)若在样本中,利用分层抽样的方法从成绩不低于70分的学生中随机抽取6人,再从中抽取3人赠送一套国学经典学籍,试求恰好抽中2名优秀生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,BC=2,点M,N分别是边AB,CD上的点,且MN∥BC,![]()
![]() .若将矩形ABCD沿MN折起使其形成60°的二面角(如图).
.若将矩形ABCD沿MN折起使其形成60°的二面角(如图).

(1)求证:平面CND⊥平面AMND;
(2)求直线MC与平面AMND所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l经过点A(﹣1,0),其倾斜角是α,以原点O为极点,以x轴的非负半轴为极轴,与直角坐标系xOy取相同的长度单位,建立极坐标系.设曲线C的极坐标方程是ρ2=6ρcosθ﹣5.
(Ⅰ)若直线l和曲线C有公共点,求倾斜角α的取值范围;
(Ⅱ)设B(x,y)为曲线C任意一点,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com