
已知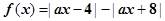 ,
, R
R
(Ⅰ)当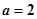 时,解不等式
时,解不等式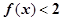 ;
;
(Ⅱ)若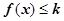 恒成立,求k的取值范围.
恒成立,求k的取值范围.
(Ⅰ){x|x>-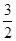 };(Ⅱ)[12,+∞).
};(Ⅱ)[12,+∞).
解析试题分析:(Ⅰ)利用分类讨论思想将函数转化为分段函数,然后逐一求解每个不等式;(Ⅱ)利用绝对值性质定理求解f(x)=|ax-4|-|ax+8|的最大值,然后确定k的取值范围.
试题解析:(Ⅰ)当a=2时,
f(x)=2(|x-2|-|x+4|)=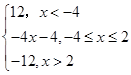
当x<-4时,不等式不成立;
当-4≤x≤2时,由-4x-4<2,得-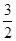 <x≤2;
<x≤2;
当x>2时,不等式必成立.
综上,不等式f(x)<2的解集为{x|x>-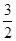 }.
}.
(Ⅱ)因为f(x)=|ax-4|-|ax+8|≤|(ax-4)-(ax+8)|=12,
当且仅当ax≤-8时取等号.
所以f(x)的最大值为12.
故k的取值范围是[12,+∞).
考点:1.绝对值不等式的解法;2.绝对值不等式的性质定理.


 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:解答题
已知关于x的不等式|ax-2|+|ax-a|≥2(a>0).
(1)当a=1时,求此不等式的解集;
(2)若此不等式的解集为R,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com