
分析 (I)化简可得(4+2d)2=4(4+6d),从而求得d=2;从而求an和Sn;
(II)可求得2Sn-5an=2[(n-1)2-6],从而化简得bn=$\left\{\begin{array}{l}{2(n+1),1≤n≤3}\\{\frac{1}{n(n+3)},n≥4}\end{array}\right.$;从而分类讨论求Tn,从而证明.
解答 解:(I)由题意知,a3=4+2d,a7=4+6d,
故(4+2d)2=4(4+6d),
解得,d=0(舍去)或d=2;
故an=4+2(n-1)=2(n+1),
Sn=$\frac{4+2n+2}{2}$n=n(n+3);
(II)证明:∵2Sn-5an=2n(n+3)-5×2(n+1)=2[(n-1)2-6],
∴当n<4时,2Sn<5an,当n≥4时,2Sn>5an;
∴bn=$\left\{\begin{array}{l}{2(n+1),1≤n≤3}\\{\frac{1}{n(n+3)},n≥4}\end{array}\right.$;
①当1≤n≤3时,
T1=4,T2=10,T3=4+6+8=18;
②当n≥4时,
Tn=18+$\frac{1}{4×7}$+$\frac{1}{5×8}$+$\frac{1}{6×9}$+$\frac{1}{7×10}$+…+$\frac{1}{n(n+3)}$,
=18+$\frac{1}{3}$($\frac{1}{4}$-$\frac{1}{7}$+$\frac{1}{5}$-$\frac{1}{8}$+$\frac{1}{6}$-$\frac{1}{9}$+$\frac{1}{7}$-$\frac{1}{10}$+…+$\frac{1}{n}$-$\frac{1}{n+3}$)
=18+$\frac{1}{3}$($\frac{1}{4}$+$\frac{1}{5}$+$\frac{1}{6}$-$\frac{1}{n+1}$-$\frac{1}{n+2}$-$\frac{1}{n+3}$)
<18+$\frac{1}{3}$($\frac{1}{4}$+$\frac{1}{5}$+$\frac{1}{6}$)=18$\frac{37}{180}$;
综上所述,4≤Tn<18$\frac{37}{180}$.
点评 本题考查了等差数列与等比数列的应用,同时考查了分类讨论的思想应用及方程思想的应用.


科目:高中数学 来源: 题型:解答题
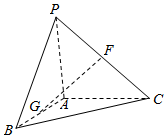 如图,在三棱锥P-ABC中,F、G、H分别是PC、AB、BC的中点,PA⊥平面ABC,PA=AB=AC=2,二面角B-PA-C为120°.
如图,在三棱锥P-ABC中,F、G、H分别是PC、AB、BC的中点,PA⊥平面ABC,PA=AB=AC=2,二面角B-PA-C为120°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
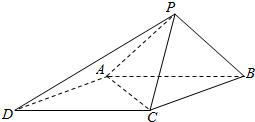 如图,已知在四陵锥P-ABCD中,底面ABCD是边长为2的菱形,∠BCD=120°,AP=BP,∠APB=90°,PC=2.
如图,已知在四陵锥P-ABCD中,底面ABCD是边长为2的菱形,∠BCD=120°,AP=BP,∠APB=90°,PC=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 1996 | D. | -1996 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 20 | C. | 256 | D. | 510 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | cosα | B. | $\frac{1}{cosα}$ | C. | -cosα | D. | -$\frac{1}{cosα}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com