练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （2013•梅州二模）若m是一个给定的正整数，如果两个整数a、b用m除所得的余数相同，则称a与b对m校同余，记作a≡b[mod（m）]，例如1≡13[mod（4）]，若22012≡r[mod（7）]，则r可能为（ ）

    A.5 B.4 C.3 D.2

     

    B

    【解析】

    试题分析：利用二项式定理得22012=4×8670=4×（7+1）670=4×[C×7670+…+C×7+C]，可知22012被7除得的余数为4，即可得到结论．

    【解析】
    由题意，22012=4×8670=4×（7+1）670=4×[C×7670+…+C×7+C]，

    ∴22012≡4（mod7），

    若22012≡r[mod（7）]，则r可能为4．

    故选B，

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：[同步]2014年新人教A版选修4-7 1.3黄金分割法-0.618法（解析版） 题型：填空题

    （选做题）用0.618法选取试点，试验区间为[2，4]，若第一个试点x1处的结果比x2处好，则第三个试点应选取在 处．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-6 4.1信息的加密与去密练习卷（解析版） 题型：填空题

    为保证信息安全，信息传输必须使用加密方式．某种初级加密，解密原理如下：明文密文密文明文．已知加密为y=ax﹣2（x为明文，y为密文），如果明文“3“通过加密后得到密文为“6“，再发送，接受方通过解密得到明文“3“，若接受方接到密文为“1022“，则原发的明文是 ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-6 2.6弃九验算法练习卷（解析版） 题型：选择题

    （2014•沈阳模拟）用“秦九韶”算法计算多项式f（x）=5x5+4x4+3x3+2x2+x+1当x=2时的值时，需要做乘法和加法的次数分别为（ ）

    A.4，4 B.4，5 C.5，4 D.5，5

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-6 2.4一次同余方程练习卷（解析版） 题型：选择题

    数80100除以9所得余数是（ ）

    A.0 B.8 C.﹣1 D.1

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-6 2.1同余练习卷（解析版） 题型：填空题

    设a、b、m（m＞0）为整数，若a和b被m除得的余数相同，则称a和b对模m同余，记为a≡b（bmodm）；已知a=1+C201+C202•2+C203•22+…+C2020•219，b≡a（bmod10），则满足条件的正整数b中，最小的两位数是 ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-6 2.1同余练习卷（解析版） 题型：选择题

    （2013•梅州二模）若m是一个给定的正整数，如果两个整数a、b用m除所得的余数相同，则称a与b对m校同余，记作a≡b[mod（m）]，例如1≡13[mod（4）]，若22012≡r[mod（7）]，则r可能为（ ）

    A.5 B.4 C.3 D.2

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-6 1.2最大公因数与最小公倍数 题型：选择题

    利用更相减损术求99，36的最大公约数的操作步骤为（99，36）→（63，36）→（27，36）→（27，9）→（18，9）→（9，9），那么99，36的最大公约数为（ ）

    A.36 B.27 C.18 D.9

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 4.2数学归纳法证明不等式举例（解析版） 题型：选择题

    用数学归纳法证明不等式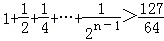成立，起始值至少应取为（ ）

    A.7 B.8 C.9 D.10

     

    查看答案和解析>>

    同步练习册答案