
设a、b、m(m>0)为整数,若a和b被m除得的余数相同,则称a和b对模m同余,记为a≡b(bmodm);已知a=1+C201+C202•2+C203•22+…+C2020•219,b≡a(bmod10),则满足条件的正整数b中,最小的两位数是 .
科目:高中数学 来源:[同步]2014年新人教A版选修4-7 1.3黄金分割法-0.618法(解析版) 题型:填空题
(2010•湖南)已知一种材料的最佳加入量在110g到210g之间,若用0.618法安排试验,则第一次试点的加入量可以是 g.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-6 4.1信息的加密与去密练习卷(解析版) 题型:填空题
(2006•宝山区二模)有一密码把英文的明文(真实文)按字母分解,其中a,b,…,z的26个字母(不论大小写)分别对应着1,2,…,26个自然数,见下表:
a | b | c | d | e | f | g | h | i | j | k | l | m |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
n | o | p | q | r | s | t | u | v | w | x | y | z |
14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
(x是奇数)(x是偶数)给出如下一个变换公式: ,如
,如 ,即h变成q.按上述规定,若将明文译成密文是shxc,那么原来的明文是 .
,即h变成q.按上述规定,若将明文译成密文是shxc,那么原来的明文是 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-6 2.4一次同余方程练习卷(解析版) 题型:填空题
(2013•永州一模)若两整数a,b除以同一个整数m,所得余数相同,则称a,b对模m同余.即当a,b,m∈z时,若 =k(k∈z,k≠0),则称a、b对模m同余,用符号a=b(modm)表示.
=k(k∈z,k≠0),则称a、b对模m同余,用符号a=b(modm)表示.
(1)若6=b(mod2)且0<b<6,则b的所有可能取值为 ;
(2)若a=10(modm)(a>10,m>1),满足条件的a由小到大依次记为a1,a2…an,…,当数列{an}前m﹣1项的和为60(m﹣1)时,则m= .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-6 2.4一次同余方程练习卷(解析版) 题型:选择题
(2013•梅州二模)若m是一个给定的正整数,如果两个整数a、b用m除所得的余数相同,则称a与b对m校同余,记作a≡b[mod(m)],例如1≡13[mod(4)],若22012≡r[mod(7)],则r可能为( )
A.5 B.4 C.3 D.2
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-6 2.1同余练习卷(解析版) 题型:选择题
设a、b、m为整数(m>0),若a和b被m除得的余数相同,则称a和b对模m同余,记为a≡b(modm).已知a=2+C +C
+C •2+C
•2+C •22+…+C
•22+…+C •219,b≡a(mon10),则b的值可以是( )
•219,b≡a(mon10),则b的值可以是( )
A.2015 B.2012 C.2008 D.2006
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 4.1数学归纳法练习卷(解析版) 题型:选择题
用数学归纳法证“1﹣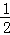 +
+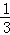 ﹣
﹣ +…+
+…+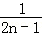 ﹣
﹣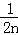 =
=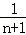 +
+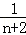 +…+
+…+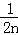 (n∈N*)”的过程中,当n=k到n=k+1时,左边所增加的项为( )
(n∈N*)”的过程中,当n=k到n=k+1时,左边所增加的项为( )
A.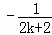 B.
B.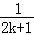 C.
C.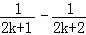 D.
D.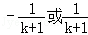
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com