
 +
+ =1(a>b>0)的左焦点为F1(-2,0),左准线l1与x轴交于点N(-3,0),过点N且倾斜角为30°的直线l交椭圆于A、B两点.
=1(a>b>0)的左焦点为F1(-2,0),左准线l1与x轴交于点N(-3,0),过点N且倾斜角为30°的直线l交椭圆于A、B两点.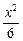 +
+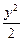 =1.
=1. (2)见解析
(2)见解析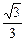 (x+3).
(x+3).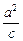 =3,解得a2=6,
=3,解得a2=6,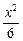 +
+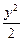 =1.
=1. (2)证明:联立方程组
(2)证明:联立方程组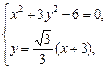
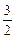 .
.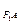 ·k
·k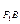 =
=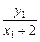 ·
·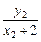 =
=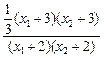
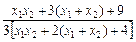 =
=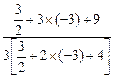 =-1,
=-1,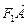 ·
·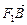 =(x1+2,y1)·(x2+2,y2)=(x1+2)(x2+2)+y1y2
=(x1+2,y1)·(x2+2,y2)=(x1+2)(x2+2)+y1y2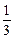 [x1x2+3(x1+x2)+9]
[x1x2+3(x1+x2)+9]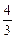 x1x2+3(x1+x2)+7=0,
x1x2+3(x1+x2)+7=0,

 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源:不详 题型:解答题
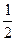 ,且过点(
,且过点(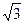 ,
,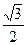 ).
). 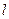 :
: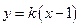 (
(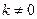 )与椭圆E交于
)与椭圆E交于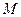 、
、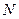 两点,证明直线
两点,证明直线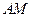 与直线
与直线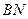 的交点在垂直于
的交点在垂直于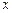 轴的定直线上,并求出该直线方程.
轴的定直线上,并求出该直线方程.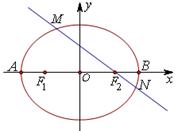
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
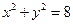 上的每一点的纵坐标压缩到原来的
上的每一点的纵坐标压缩到原来的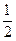 ,对应的横坐标不变,得到曲线C;设
,对应的横坐标不变,得到曲线C;设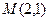 ,平行于OM的直线
,平行于OM的直线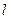 在y轴上的截距为m(m≠0),直线
在y轴上的截距为m(m≠0),直线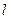 与曲线C交于A、B两个不同点.
与曲线C交于A、B两个不同点.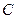 的方程;
的方程;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com