练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在直角坐标系中，曲线的参数方程为（为参数），以原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为（为实数）.

    （1）求曲线的普通方程与曲线的直角坐标方程；

    （2）当时，设、分别为曲线和曲线上的动点，求的最小值.

    【答案】（1），；（2）.

    【解析】

    （1）在曲线的参数方程中消去参数可得出曲线的普通方程，将曲线的极坐标方程变形为，进而可得出曲线的直角坐标方程；

    （2）设点的坐标为，利用点到直线的距离公式结合正弦函数的有界性可求得的最小值.

    （1）将曲线的参数方程变形为，可得，

    将曲线的极坐标方程变形为，即，

    所以，曲线的直角坐标方程为.

    因此，曲线的普通方程为，曲线的直角坐标方程为；

    （2）当时，直线的方程为.

    设点，则点到直线的距离为，

    其中为锐角，且.

    当时，取得最小值.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】新型冠状病毒肺炎COVID-19疫情发生以来，在世界各地逐渐蔓延．在全国人民的共同努力和各级部门的严格管控下，我国的疫情已经得到了很好的控制．然而，每个国家在疫情发生初期，由于认识不足和措施不到位，感染确诊人数都会出现加速增长．如表是小王同学记录的某国从第一例新型冠状病毒感染确诊之日开始，连续8天每日新型冠状病毒感染确诊的累计人数．

    日期代码

    1

    2

    3

    4

    5

    6

    7

    8

    累计确诊人数

    4

    8

    16

    31

    51

    71

    97

    122

    为了分析该国累计感染确诊人数的变化趋势，小王同学分别用两种模型：

    ①，②对变量和的关系进行拟合，得到相应的回归方程并进行残差分析，残差图如下（注：残差，且经过计算得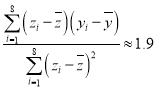，，其中，，

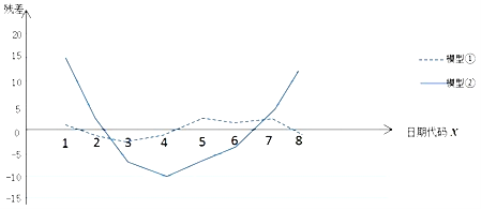
    （1）根据残差图，比较模型①，②的拟合效果，应该选择哪个模型？并简要说明理由；

    （2）根据（1）中选定的模型求出相应的回归方程；

    （3）如果第9天该国仍未采取有效的防疫措施，试根据（2）中所求的回归方程估计该国第9天新型冠状病毒感染确诊的累计人数．（结果保留为整数）

    附：回归直线的斜率和截距的最小二乘估计公式分别为：，．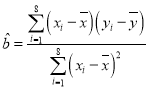

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系xOy中，曲线E的参数方程为（为参数），以O为极点，x轴非负半轴为极轴建立极坐标系，直线，的极坐标方程分别为，，交曲线E于点A，B，交曲线E于点C，D.

    （1）求曲线E的普通方程及极坐标方程；

    （2）求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】向50名学生调查对A、B两事件的态度，有如下结果：赞成A的人数是全体的五分之三，其余的不赞成，赞成B的比赞成A的多3人，其余的不赞成；另外，对A、B都不赞成的学生数比对A、B都赞成的学生数的三分之一多1人. 问对A、B都赞成的学生有____________人

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝ax2－(a2＋b)x＋aln x(a，b∈R)．

    (Ⅰ)当b＝1时，求函数f(x)的单调区间；

    (Ⅱ)当a＝－1，b＝0时，证明：f(x)＋ex>－x2－x＋1(其中e为自然对数的底数)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为迎接“五一国际劳动节”，某商场规定购买超过6000元商品的顾客可以参与抽奖活动现有甲品牌和乙品牌的扫地机器人作为奖品，从这两种品牌的扫地机器人中各随机抽取6台检测它们充满电后的工作时长相关数据见下表（工作时长单位：分）

    机器序号

    1

    2

    3

    4

    5

    6

    甲品牌工作时长/分

    220

    180

    210

    220

    200

    230

    乙品牌工作时长/分

    200

    190

    240

    230

    220

    210

    （1）根据所提供的数据，计算抽取的甲品牌的扫地机器人充满电后工作时长的平均数与方差；

    （2）从乙品牌被抽取的6台扫地机器人中随机抽出3台扫地机器人，记抽出的扫地机器人充满电后工作时长不低于220分钟的台数为，求的分布列与数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，曲线的参数方程(为参数)，直线的参数方程(为参数).

    （1）求曲线在直角坐标系中的普通方程；

    （2）以坐标原点为极点，轴的正半轴为极轴建立极坐标系，当曲线截直线所得线段的中点极坐标为时，求直线的倾斜角.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱柱侧面．

    (1)求证：平面平面；

    (2)若，求二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）＝sin（ωx+φ）（ω＞0，）的最小正周期为π，且关于中心对称，则下列结论正确的是（ ）

    A.f（1）＜f（0）＜f（2）B.f（0）＜f（2）＜f（1）

    C.f（2）＜f（0）＜f（1）D.f（2）＜f（1）＜f（0）

    查看答案和解析>>

    同步练习册答案