解:(I)令P(x
1,y
1),,Q(x
2,y
2),由题意,可设抛物线方程为 y
2=2px
由椭圆的方程可得F
1 (-1,0),F
2 (1,0 )故p=2,曲线C的方程为 y
2=4x,
由题意,可设PQ的方程 x=my-1 (m>0).把PQ的方程代入曲线C的方程 化简可得 y
2-4my+4=0,
∴y
1+y
2=4m,y
1y
2=4. 又
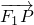
=
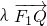
,∴x
1+1=λ(x
2+1),y
1=λy
2,
又
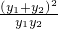
=λ+

+2=4m
2.λ∈[2,4],∴2+

≤λ+

≤4+

,

≤m
2≤

,
∴

≤

≤

∴直线L的斜率k的取值范围为[

,

].
(II)由于P,M关于X轴对称,故M(x
1,-y
1),,
∵

-

=
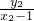
+
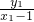
=

=0,
∴M、Q、F
2三点共线,故直线MQ过定点 F
2 (1,0 ).
分析:(I)求出曲线C的方程,把PQ的方程 x=my-1 (m>0)代入曲线C的方程 化简可得 y
2-4my+4=0,利用根与系数的关系 及
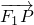
=
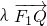
,可得
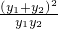
=λ+

+2=4m
2,据λ∈[2,4],求得直线L的斜率

的范围.
(II)根据
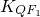
-

=0,可得 M、Q、F
2三点共线,故直线MQ过定点 F
2 (1,0 ).
点评:本题考查椭圆、抛物线的标准方程、简单性质,三点共线的条件,根据题意,得到2+

≤λ+

≤4+

,是解题的关键.

 +
+ =1的左、右焦点,曲线C是坐标原点为顶点,以F2为焦点的抛物线,过点F1的直线l交曲线C于x轴上方两个不同点P、Q,点P关于x轴的对称点为M,设
=1的左、右焦点,曲线C是坐标原点为顶点,以F2为焦点的抛物线,过点F1的直线l交曲线C于x轴上方两个不同点P、Q,点P关于x轴的对称点为M,设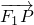 =
=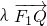
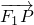 =
=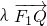 ,∴x1+1=λ(x2+1),y1=λy2,
,∴x1+1=λ(x2+1),y1=λy2,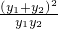 =λ+
=λ+ +2=4m2.λ∈[2,4],∴2+
+2=4m2.λ∈[2,4],∴2+ ≤λ+
≤λ+ ≤4+
≤4+ ,
, ≤m2≤
≤m2≤ ,
, ≤
≤ ≤
≤ ∴直线L的斜率k的取值范围为[
∴直线L的斜率k的取值范围为[ ,
, ].
]. -
- =
=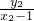 +
+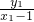 =
= =0,
=0,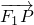 =
=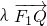 ,可得
,可得 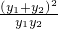 =λ+
=λ+ +2=4m2,据λ∈[2,4],求得直线L的斜率
+2=4m2,据λ∈[2,4],求得直线L的斜率  的范围.
的范围.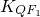 -
- =0,可得 M、Q、F2三点共线,故直线MQ过定点 F2 (1,0 ).
=0,可得 M、Q、F2三点共线,故直线MQ过定点 F2 (1,0 ). ≤λ+
≤λ+ ≤4+
≤4+ ,是解题的关键.
,是解题的关键. 

 如图,已知F1,F2分别是椭圆C:
如图,已知F1,F2分别是椭圆C: