分析 （1）由圆x2+y2=$\frac{2}{3}$与椭圆C的四个顶点构成的四边形相切得到a，b的关系式，结合c=1及隐含条件求得a，b的值，则椭圆方程可求；
（2）当直线l的斜率不存在时，直接求出$\frac{1}{|MF|}$+$\frac{1}{|NF|}$的值，当直线l的斜率存在时，设出直线l的方程，与椭圆方程联立，利用根与系数的关系求出M，N的横坐标的和与积，代入$\frac{1}{|MF|}$+$\frac{1}{|NF|}$整理得答案．
解答 
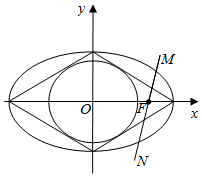（1）解：过（a，0）与（0，b）的直线方程为$\frac{x}{a}+\frac{y}{b}=1$
即bx+ay-ab=0，
由圆x2+y2=$\frac{2}{3}$与直线bx+ay-ab=0相切，得$\frac{|-ab|}{\sqrt{{a}^{2}+{b}^{2}}}=\frac{\sqrt{6}}{3}$，
又c=1，a2=b2+c2，联立可得a2=2，b2=1，
∴椭圆C的方程为$\frac{{x}^{2}}{2}+{y}^{2}=1$；
（2）证明：当直线l的斜率不存在时，MN所在直线方程为x=1，代入椭圆$\frac{{x}^{2}}{2}+{y}^{2}=1$，
解得y=$±\frac{\sqrt{2}}{2}$，即|MF|=|NF|=$\frac{\sqrt{2}}{2}$，
此时$\frac{1}{|MF|}$+$\frac{1}{|NF|}$=2$\sqrt{2}$；
当直线l的斜率存在时，设直线方程为y=k（x-1），
联立$\left\{\begin{array}{l}{y=k（x-1）}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$，可得（1+2k2）x2-4k2x+2k2-2=0．
设M（x1，y1），N（x2，y2），
则${x}_{1}+{x}_{2}=\frac{4{k}^{2}}{1+2{k}^{2}}，{x}_{1}{x}_{2}=\frac{2{k}^{2}-2}{1+2{k}^{2}}$，
又|MF|=$\sqrt{2}-\frac{\sqrt{2}}{2}{x}_{1}$，|NF|=$\sqrt{2}-\frac{\sqrt{2}}{2}{x}_{2}$，
∴$\frac{1}{|MF|}$+$\frac{1}{|NF|}$=$\frac{1}{\sqrt{2}-\frac{\sqrt{2}}{2}{x}_{1}}+\frac{1}{\sqrt{2}-\frac{\sqrt{2}}{2}{x}_{2}}$=$\frac{2\sqrt{2}-\frac{\sqrt{2}}{2}（{x}_{1}+{x}_{2}）}{（\sqrt{2}-\frac{\sqrt{2}}{2}{x}_{1}）（\sqrt{2}-\frac{\sqrt{2}}{2}{x}_{2}）}$
=$\frac{2\sqrt{2}-\frac{\sqrt{2}}{2}•\frac{4{k}^{2}}{1+2{k}^{2}}}{2-\frac{4{k}^{2}}{1+2{k}^{2}}+\frac{1}{2}•\frac{2{k}^{2}-2}{1+2{k}^{2}}}$=$\frac{2\sqrt{2}（{k}^{2}+1）}{{k}^{2}+1}=2\sqrt{2}$．
点评 本题考查椭圆方程的求法，考查了椭圆的简单性质，训练了直线与圆锥曲线位置关系问题的解决方法，考查了运算能力，属中档题，本题解答中用到焦半径公式，使用答案时要注意研究其导出的方法．
阅读快车系列答案科目：高中数学 来源： 题型：填空题
查看答案和解析>>
科目：高中数学 来源： 题型：选择题
| A． | $\frac{3}{2}$ | B． | -$\frac{3}{2}$ | C． | ±$\frac{3}{2}$ | D． | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com